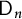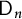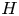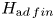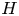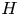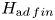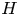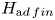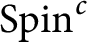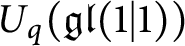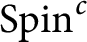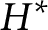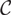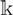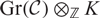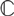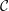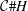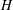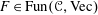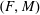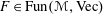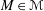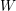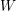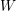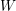Refine listing
Actions for selected content:
71 results in 16Txx
McKay matrices for finite-dimensional Hopf algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2021, pp. 686-731
- Print publication:
- June 2022
-
- Article
- Export citation
EXAMPLES OF FINITE-DIMENSIONAL POINTED HOPF ALGEBRAS IN CHARACTERISTIC 2
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 01 December 2020, pp. 65-78
- Print publication:
- January 2022
-
- Article
- Export citation
On the adjoint representation of a hopf algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 11 November 2020, pp. 1092-1099
-
- Article
- Export citation
Kuperberg invariants for balanced sutured 3-manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 1698-1742
- Print publication:
- December 2021
-
- Article
- Export citation
THE CASIMIR NUMBER AND THE DETERMINANT OF A FUSION CATEGORY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 August 2020, pp. 438-450
- Print publication:
- May 2021
-
- Article
- Export citation
GENERALISED QUANTUM DETERMINANTAL RINGS ARE MAXIMAL ORDERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 04 August 2020, pp. 515-525
- Print publication:
- September 2021
-
- Article
- Export citation
One-generator braces and indecomposable set-theoretic solutions to the Yang–Baxter equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 06 May 2020, pp. 676-696
-
- Article
- Export citation
(WEAK) INCIDENCE BIALGEBRAS OF MONOIDAL CATEGORIES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 16 March 2020, pp. 139-157
- Print publication:
- January 2021
-
- Article
-
- You have access
- Open access
- Export citation
Extensions of tensor categories by finite group fusion categories
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 11 November 2019, pp. 161-189
- Print publication:
- January 2021
-
- Article
- Export citation
QUANTUM INCREASING SEQUENCES GENERATE QUANTUM PERMUTATION GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 631-639
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
COALTERNATIVE COALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 20 August 2019, pp. S142-S164
- Print publication:
- December 2020
-
- Article
- Export citation
Cohomology of Modules Over
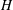 $H$-categories and Co-
$H$-categories and Co-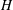 $H$-categories
$H$-categories
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 06 August 2019, pp. 1352-1385
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Actions of skew braces and set-theoretic solutions of the reflection equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 25 June 2019, pp. 1089-1113
-
- Article
- Export citation
AN IDENTITY OF PARABOLIC KAZHDAN–LUSZTIG POLYNOMIALS ARISING FROM SQUARE-IRREDUCIBLE MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 30 April 2019, pp. 81-93
- Print publication:
- February 2021
-
- Article
- Export citation
On Structure Groups of Set-Theoretic Solutions to the Yang–Baxter Equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 683-717
-
- Article
- Export citation
Monoidal Categories, 2-Traces, and Cyclic Cohomology
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 293-312
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
A CLASS OF QUASITRIANGULAR GROUP-COGRADED MULTIPLIER HOPF ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 20 December 2018, pp. 43-57
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
Left Braces and the Quantum Yang–Baxter Equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 595-608
-
- Article
- Export citation
ON CANONICAL BASES AND INDUCTION OF
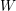 $W$-GRAPHS
$W$-GRAPHS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 17 July 2018, pp. 1-41
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
Liftings of Jordan and Super Jordan Planes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 3 / August 2018
- Published online by Cambridge University Press:
- 12 April 2018, pp. 661-672
-
- Article
- Export citation