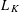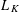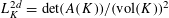Refine listing
Actions for selected content:
52 results in 49Kxx
Lower semi-continuity for non-coercive polyconvex integrals in the limit case*
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 10 December 2015, pp. 243-264
- Print publication:
- April 2016
-
- Article
- Export citation
A SIMPLICIAL POLYTOPE THAT MAXIMIZES THE ISOTROPIC CONSTANT MUST BE A SIMPLEX
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 May 2015, pp. 307-320
- Print publication:
- 2016
-
- Article
- Export citation
Rational functions with maximal radius of absolute monotonicity
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 May 2014, pp. 159-205
-
- Article
-
- You have access
- Export citation
DETERMINATION OF JOIN REGIONS BETWEEN CARBON NANOSTRUCTURES USING VARIATIONAL CALCULUS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 4 / April 2013
- Published online by Cambridge University Press:
- 04 September 2013, pp. 221-247
-
- Article
-
- You have access
- Export citation
GLOBAL SOLUTIONS OF THE EQUATION OF THE KIRCHHOFF ELASTIC ROD IN SPACE FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 27 September 2012, pp. 70-80
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
LOWER SEMICONTINUITY OF PARAMETRIC GENERALIZED WEAK VECTOR EQUILIBRIUM PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 02 October 2009, pp. 85-95
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
THE FILLED INELASTIC MEMBRANE: A SET OF CHALLENGING PROBLEMS IN THE CALCULUS OF VARIATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 02 July 2009, pp. 506-509
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
Optimal boarding policies for thin passengers
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1098-1114
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Optimal dividend payments until ruin of diffusion processes when payments are subject to both fixed and proportional costs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 39 / Issue 3 / September 2007
- Published online by Cambridge University Press:
- 01 July 2016, pp. 669-689
- Print publication:
- September 2007
-
- Article
-
- You have access
- Export citation
Elastica in SO(3)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 105-124
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
Lagrangian conditions for a nonsmooth vector-valued minimax
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 2 / October 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 163-175
- Print publication:
- October 1998
-
- Article
-
- You have access
- Export citation
Optimality of the round-robin routing policy
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 31 / Issue 2 / June 1994
- Published online by Cambridge University Press:
- 14 July 2016, pp. 466-475
- Print publication:
- June 1994
-
- Article
- Export citation