Refine listing
Actions for selected content:
50 results in 49Qxx
Double Γ-Convergence and Application to Energy Functionals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 28 July 2014, pp. 107-124
-
- Article
-
- You have access
- Export citation
A VARIATIONAL APPROACH FOR ONE-DIMENSIONAL PRESCRIBED MEAN CURVATURE PROBLEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 145-161
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
CONNECTEDNESS AND MINIMAL LENGTH ELEMENTS IN SPACES OF BOUNDED CURVATURE PATHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 174-176
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
A GEOMETRIC STUDY OF WASSERSTEIN SPACES: ULTRAMETRICS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 27 May 2014, pp. 162-178
- Print publication:
- January 2015
-
- Article
- Export citation
On Hölder continuity-in-time of the optimal transport map towards measures along a curve
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 31 March 2011, pp. 401-409
-
- Article
-
- You have access
- Export citation
ON THE MAXIMIZATION OF A CLASS OF FUNCTIONALS ON CONVEX REGIONS, AND THE CHARACTERIZATION OF THE FARTHEST CONVEX SET
- Part of
-
- Journal:
- Mathematika / Volume 56 / Issue 2 / July 2010
- Published online by Cambridge University Press:
- 18 May 2010, pp. 245-265
- Print publication:
- July 2010
-
- Article
- Export citation
Elastica in SO(3)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 1 / August 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 105-124
- Print publication:
- August 2007
-
- Article
-
- You have access
- Export citation
Distribution-Invariant Risk Measures, Entropy, and Large Deviations
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 1 / March 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 16-40
- Print publication:
- March 2007
-
- Article
-
- You have access
- Export citation
The double cover relative to a convex domain and the relative isoperimetric inequality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 375-382
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
The isoperimetric problem on some singular surfaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 2 / April 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 167-197
- Print publication:
- April 2005
-
- Article
-
- You have access
- Export citation
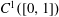
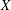
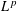
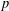
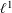
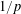

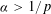
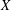
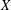
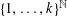
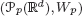 ). We prove that in most cases such a map is no more than 1/
). We prove that in most cases such a map is no more than 1/