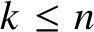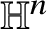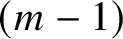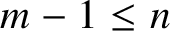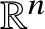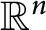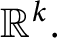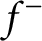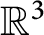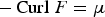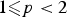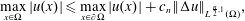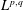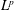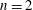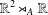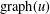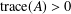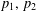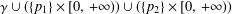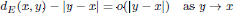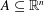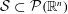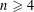Refine listing
Actions for selected content:
50 results in 49Qxx
Lipschitz graphs and currents in Heisenberg groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 February 2022, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Three candidate plurality is stablest for small correlations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 28 September 2021, e65
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nontame Morse–Smale flows and odd Chern–Weil theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 06 July 2021, pp. 1579-1624
- Print publication:
- December 2022
-
- Article
- Export citation
Tight frames and related geometric problems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 18 December 2020, pp. 942-963
- Print publication:
- December 2021
-
- Article
- Export citation
Optimal free export/import regions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 17 September 2020, pp. 737-751
- Print publication:
- December 2021
-
- Article
- Export citation
Reflection of Willmore Surfaces with Free Boundaries
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 11 March 2020, pp. 787-804
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analytic and geometric properties of dislocation singularities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 01 February 2019, pp. 1609-1651
- Print publication:
- August 2020
-
- Article
- Export citation
An Endpoint Alexandrov Bakelman Pucci Estimate in the Plane
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 11 January 2019, pp. 643-651
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
On the boundary regularity of phase-fields for Willmore's energy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1017-1035
- Print publication:
- August 2019
-
- Article
- Export citation
Reverse Faber–Krahn and Mahler inequalities for the Cheeger constant
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 913-937
- Print publication:
- October 2018
-
- Article
- Export citation
Flows of measures generated by vector fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 14 February 2018, pp. 773-818
- Print publication:
- August 2018
-
- Article
- Export citation
Dynamics of an Innovation Diffusion Model with Time Delay
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 07 September 2017, pp. 455-481
- Print publication:
- August 2017
-
- Article
- Export citation
Curvature-dependent energies: a geometric and analytical approach
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 27 February 2017, pp. 449-503
- Print publication:
- June 2017
-
- Article
- Export citation
A general formula for the anisotropic outer Minkowski content of a set
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 393-413
- Print publication:
- April 2016
-
- Article
- Export citation
THE MEAN CURVATURE EQUATION ON SEMIDIRECT PRODUCTS
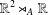 $\mathbb{R}^{2}\rtimes _{A}\mathbb{R}$: HEIGHT ESTIMATES AND SCHERK-LIKE GRAPHS
$\mathbb{R}^{2}\rtimes _{A}\mathbb{R}$: HEIGHT ESTIMATES AND SCHERK-LIKE GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 26 February 2016, pp. 118-144
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
Some new results about the geometry of sets of finite perimeter
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 23 December 2015, pp. 79-105
- Print publication:
- February 2016
-
- Article
- Export citation
LOCAL SET APPROXIMATION: MATTILA–VUORINEN TYPE SETS, REIFENBERG TYPE SETS, AND TANGENT SETS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 30 October 2015, e24
-
- Article
-
- You have access
- Open access
- Export citation
Stress constraints in simple bodies undergoing large strains: a variational approach
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 22 October 2015, pp. 1183-1214
- Print publication:
- December 2015
-
- Article
- Export citation
Convolution estimates for singular measures and some global nonlinear Brascamp—Lieb inequalities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 08 October 2015, pp. 1223-1237
- Print publication:
- December 2015
-
- Article
- Export citation
CHARACTERIZATIONS OF RICCI FLAT METRICS AND LAGRANGIAN SUBMANIFOLDS IN TERMS OF THE VARIATIONAL PROBLEM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 643-651
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation