Let X be a continuous-time strongly mixing or weakly dependent process and let T be a renewal process independent of X. We show general conditions under which the sampled process $(X_{T_i},T_i-T_{i-1})^{\top}$ is strongly mixing or weakly dependent. Moreover, we explicitly compute the strong mixing or weak dependence coefficients of the renewal sampled process and show that exponential or power decay of the coefficients of X is preserved (at least asymptotically). Our results imply that essentially all central limit theorems available in the literature for strongly mixing or weakly dependent processes can be applied when renewal sampled observations of the process X are at our disposal.

Pareto distribution is an important distribution in extreme value theory. In this paper, we consider parallel systems with Pareto components and study the effect of heterogeneity on skewness of such systems. It is shown that, when the lifetimes of components have different shape parameters, the parallel system with heterogeneous Pareto component lifetimes is more skewed than the system with independent and identically distributed Pareto components. However, for the case when the lifetimes of components have different scale parameters, the result gets reversed in the sense of star ordering. We also establish the relation between star ordering and dispersive ordering by extending the result of Deshpande and Kochar [(1983). Dispersive ordering is the same as tail ordering. Advances in Applied Probability 15(3): 686–687] from support $(0, \infty )$ to general supports $(a, \infty )$, $a > 0$. As a consequence, we obtain some new results on dispersion of order statistics from heterogeneous Pareto samples with respect to dispersive ordering.

We introduce a multivariate class of distributions with support I, a k-orthotope in $[0,\infty)^{k}$, which is dense in the set of all k-dimensional distributions with support I. We call this new class ‘multivariate finite-support phase-type distributions’ (MFSPH). Though we generally define MFSPH distributions on any finite k-orthotope in $[0,\infty)^{k}$, here we mainly deal with MFSPH distributions with support $[0,1)^{k}$. The distribution function of an MFSPH variate is computed by using that of a variate in the MPH$^{*} $ class, the multivariate class of distributions introduced by Kulkarni (1989). The marginal distributions of MFSPH variates are found as FSPH distributions, the class studied by Ramaswami and Viswanath (2014). Some properties, including the mixture property, of MFSPH distributions are established. Estimates of the parameters of a particular class of bivariate finite-support phase-type distributions are found by using the expectation-maximization algorithm. Simulated samples are used to demonstrate how this class could be used as approximations for bivariate finite-support distributions.

We consider coherent systems with independent and identically distributed components. While it is clear that the system’s life will be stochastically larger when the components are replaced with stochastically better components, we show that, in general, similar results may not hold for hazard rate, reverse hazard rate, and likelihood ratio orderings. We find sufficient conditions on the signature vector for these results to hold. These results are combined with other well-known results in the literature to get more general results for comparing two systems of the same size with different signature vectors and possibly with different independent and identically distributed component lifetimes. Some numerical examples are also provided to illustrate the theoretical results.

Let x denote a vector of length q consisting of 0s and 1s. It can be interpreted as an ‘opinion’ comprised of a particular set of responses to a questionnaire consisting of q questions, each having {0, 1}-valued answers. Suppose that the questionnaire is answered by n individuals, thus providing n ‘opinions’. Probabilities of the answer 1 to each question can be, basically, arbitrary and different for different questions. Out of the 2q different opinions, what number, μn , would one expect to see in the sample? How many of these opinions, μn (k), will occur exactly k times? In this paper we give an asymptotic expression for μn / 2q and the limit for the ratios μn (k)/μn , when the number of questions q increases along with the sample size n so that n = λ2q , where λ is a constant. Let p(x ) denote the probability of opinion x . The key step in proving the asymptotic results as indicated is the asymptotic analysis of the joint behaviour of the intensities np(x ). For example, one of our results states that, under certain natural conditions, for any z > 0, ∑1 {np( x) > z} = d n z −u ,d n = o(2q ).

In this paper, some ordering properties of convolutions of heterogeneous Bernoulli random variables are discussed. It is shown that, under some suitable conditions, the likelihood ratio order and the reversed hazard rate order hold between convolutions of two heterogeneous Bernoulli sequences. The results established here extend and strengthen the previous results of Pledger and Proschan (1971) and Boland, Singh and Cukic (2002).

Kochar and Xu (2009) proved that a parallel system with heterogeneous exponential component lifetimes is more skewed (according to the convex transform order) than the system with independent and identically distributed exponential components. In this paper we extend this study to the general k-out-of-n systems for the case when there are only two types of component in the system. An open problem proposed in Pǎltǎnea (2008) is partially solved.

A parallel system with heterogeneous exponential component lifetimes is shown to be more skewed (according to the convex transform order) than the system with independent and identically distributed exponential components. As a consequence, equivalent conditions for comparing the variabilities of the largest order statistics from heterogeneous and homogeneous exponential samples in the sense of the dispersive order and the right-spread order are established. A sufficient condition is also given for the proportional hazard rate model.

Large deviation estimates are derived for sums of random variables with certain dependence structures, including finite population statistics and random graphs. The argument is based on Stein's method, but with a novel modification of Stein's equation inspired by the Cramér transform.

The simulation of distributions of financial assets is an important issue for financial institutions. If risk measures are evaluated for a simulated distribution instead of the model-implied distribution, the errors in the risk measurements need to be analyzed. For distribution-invariant risk measures which are continuous on compacts, we employ the theory of large deviations to study the probability of large errors. If the approximate risk measurements are based on the empirical distribution of independent samples, then the rate function equals the minimal relative entropy under a risk measure constraint. We solve this minimization problem explicitly for shortfall risk and average value at risk.

Stratified and simple random sampling (or testing) are two common methods used to investigate the number or proportion of items in a population with a particular attribute. Although it is known that cost factors and information about the strata in the population are often crucial in deciding whether to use stratified or simple random sampling in a given situation, the stochastic precedence ordering for random variables can also provide the basis for an interesting criteria under which these methods may be compared. It may be particularly relevant when we are trying to find as many special items as possible in a population (for example individuals with a disease in a country). Properties of this total stochastic order on the class of random variables are discussed, and necessary and sufficient conditions are established which allow the comparison of the number of items of interest found in stratified random sampling with the number found in simple random sampling in the stochastic precedence order. These conditions are compared with other results established on stratified and simple random sampling (testing) using different stochastic-order-type criteria, and applications are given for the comparison of sums of Bernoulli random variables and binomial distributions.

Our aim is to estimate the volume-weighted mean of the volumes of three-dimensional ‘particles’ (compact, not-necessarily-convex subsets) from plane sections of the particle population. The standard stereological technique is to place test lines in the plane section, and measure cubed intercept lengths with the two-dimensional particle profiles. This paper discusses more efficient estimators obtained by integrating over all possible placements of the test line. We prove that these estimators have smaller variance than the line transect estimators, and indeed are related to them by the Rao-Blackwell process. In the improved estimators, the cubed intercept length is replaced by a moment of the distance between two points in the section profile. This can be computed as a moment of the set covariance function, which in turn is computable using the fast Fourier transform. We also derive an isoperimetric-type inequality between the improved estimator and the area-weighted 3/2th moment of the profile areas. Finally, we present two practical applications to particles of silicon carbide and to synaptic boutons in brain tissue. We estimate the variance of the technique and the gain in efficiency over line transect techniques; the efficiency improvement appears to be as much as one order of magnitude.

Let X 1,…,X n be independent exponential random variables with X i having hazard rate 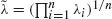. Let Y 1,…,Y n be a random sample of size n from an exponential distribution with common hazard rate ̃λ = (∏i=1 n λi )1/n , the geometric mean of the λis. Let X n:n = max{X 1,…,X n }. It is shown that X n:n is greater than Y n:n according to dispersive as well as hazard rate orderings. These results lead to a lower bound for the variance of X n:n and an upper bound on the hazard rate function of X n:n in terms of 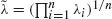. These bounds are sharper than those obtained by Dykstra et al. ((1997), J. Statist. Plann. Inference65, 203–211), which are in terms of the arithmetic mean of the λi s. Furthermore, let X 1 *,…,X n ∗ be another set of independent exponential random variables with X i ∗ having hazard rate λi ∗, i = 1,…,n. It is proved that if (logλ1,…,logλn ) weakly majorizes (logλ1 ∗,…,logλn ∗, then X n:n is stochastically greater than X n:n ∗.

In machine vision, objects are observed subject to an unknown projective transformation, and it is usual to use projective invariants for either testing for a false alarm or for classifying an object. For four collinear points, the cross-ratio is the simplest statistic which is invariant under projective transformations. We obtain the distribution of the cross-ratio under the Gaussian error model with different means. The case of identical means, which has appeared previously in the literature, is derived as a particular case. Various alternative forms of the cross-ratio density are obtained, e.g. under the Casey arccos transformation, and under an arctan transformation from the real projective line of cross-ratios to the unit circle. The cross-ratio distributions are novel to the probability literature; surprisingly various types of Cauchy distribution appear. To gain some analytical insight into the distribution, a simple linear-ratio is also introduced. We also give some results for the projective invariants of five coplanar points. We discuss the general moment properties of the cross-ratio, and consider some inference problems, including maximum likelihood estimation of the parameters.

A version of the Rao–Blackwell theorem is shown to apply to most, but not all, stereological sampling designs. Estimators based on random test grids typically have larger variance than quadrat estimators; random s-dimensional samples are worse than random r-dimensional samples for s < r. Furthermore, the standard stereological ratio estimators of different dimensions are canonically related to each other by the Rao–Blackwell process. However, there are realistic cases where sampling with a lower-dimensional probe increases efficiency. For example, estimators based on (conditionally) non-randomised test point grids may have smaller variance than quadrat estimators. Relative efficiency is related to issues in geostatistics and the theory of wide-sense stationary random fields. A uniform minimum variance unbiased estimator typically does not exist in our context.