Refine listing
Actions for selected content:
77 results in 53Bxx
Première classe de Stiefel–Whitney des espaces d'applications stables réelles en genre zéro vers une surface convexe
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 15 December 2008, pp. 383-414
- Print publication:
- April 2009
-
- Article
- Export citation
SPACE-LIKE HYPERSURFACES IN LOCALLY SYMMETRIC LORENTZ SPACE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 1 / July 2008
- Published online by Cambridge University Press:
- 01 July 2008, pp. 1-11
-
- Article
-
- You have access
- Export citation
PINCHING THEOREMS FOR A COMPACT MINIMAL SUBMANIFOLD IN A COMPLEX PROJECTIVE SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 99-114
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
CHARACTERIZATIONS OF HYPERSURFACES OF TYPE A2 IN A COMPLEX PROJECTIVE SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 1-8
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
A system of PDEs for Riemannian spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 2 / April 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-262
- Print publication:
- April 2007
-
- Article
-
- You have access
- Export citation
Ricci curvature of submanifolds in Sasakian space forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 247-256
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Osserman pseudo-Riemannian manifolds of signature (2,2)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 367-396
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
8-dimensional Einstein-Thorpe manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 2 / April 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 278-284
- Print publication:
- April 2000
-
- Article
-
- You have access
- Export citation
On 4-dimensional generalized complex space forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 379-387
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
Invariant submanifolds in flow geometry
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 290-314
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
On O. Bonnet III-isometry of surfaces in three dimensional Euclidean space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-110
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
A note on real hypersurfaces of a complex projective space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 108-113
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
Complete hypersurfaces in cylinders
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 313-318
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
On concircular transformations in Riemannian spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 218-225
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
Totally umbilical submanifolds in irreducible symmetric spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 3 / June 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 332-338
- Print publication:
- June 1982
-
- Article
-
- You have access
- Export citation
Classification of totally umbilical submanifolds in symmetric spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 2 / December 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-136
- Print publication:
- December 1980
-
- Article
-
- You have access
- Export citation
Totally umbilical submanifolds of quaternion-space-forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 26 / Issue 2 / September 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 154-162
- Print publication:
- September 1978
-
- Article
-
- You have access
- Export citation
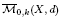 carries different real structures induced by
carries different real structures induced by 