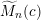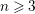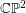Refine listing
Actions for selected content:
77 results in 53Bxx
On the total mean curvature of a compact space-like submanifold in Lorentz–Minkowski spacetime
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 October 2017, pp. 199-210
- Print publication:
- February 2018
-
- Article
- Export citation
LEVI-UMBILICAL REAL HYPERSURFACES IN A COMPLEX SPACE FORM
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 15 December 2016, pp. 99-112
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
ON THE UMBILICITY OF HYPERSURFACES IN THE HYPERBOLIC SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 16 November 2016, pp. 45-58
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Minkowski Symmetry Sets of Plane Curves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 19 May 2016, pp. 461-480
-
- Article
- Export citation
Curvature and the c-projective mobility of Kähler metrics with hamiltonian 2-forms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 8 / August 2016
- Published online by Cambridge University Press:
- 26 April 2016, pp. 1555-1575
- Print publication:
- August 2016
-
- Article
- Export citation
SOME CLASSIFICATIONS OF LORENTZIAN SURFACES WITH FINITE TYPE GAUSS MAP IN THE MINKOWSKI 4-SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 13 August 2015, pp. 415-427
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
KÄHLER SURFACES WITH QUASI CONSTANT HOLOMORPHIC CURVATURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 503-512
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
A Decomposition Theorem for Immersions of Product Manifolds
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 17 April 2015, pp. 247-269
-
- Article
- Export citation
REMARKS ON BIANCHI SUMS AND PONTRJAGIN CLASSES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 24 September 2014, pp. 365-382
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
SPECIAL HERMITIAN MANIFOLDS AND THE 1-COSYMPLECTIC HYPERSURFACES AXIOM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 504-509
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
SLANT CURVES AND PARTICLES IN THREE-DIMENSIONAL WARPED PRODUCTS AND THEIR LANCRET INVARIANTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 19 October 2012, pp. 128-142
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
Medians and means in Finsler geometry
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 February 2012, pp. 23-37
-
- Article
-
- You have access
- Export citation
FOURTH ORDER GEOMETRIC EVOLUTION EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 18 November 2010, pp. 523-524
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
ON EXTRINSICALLY SYMMETRIC HYPERSURFACES OF ℍn×ℝ
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 27 September 2010, pp. 390-400
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Gray identities, canonical connection and integrability
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 3 / October 2010
- Published online by Cambridge University Press:
- 12 August 2010, pp. 657-674
-
- Article
-
- You have access
- Export citation
A surface that contains many Lorentzian circles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 293-298
-
- Article
-
- You have access
- Export citation
The Weitzenböck machine
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 2 / March 2010
- Published online by Cambridge University Press:
- 23 February 2010, pp. 507-540
- Print publication:
- March 2010
-
- Article
-
- You have access
- Export citation
RANDERS METRICS OF SCALAR FLAG CURVATURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 15 December 2009, pp. 359-370
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
REAL HYPERSURFACES WITH CYCLIC-PARALLEL STRUCTURE JACOBI OPERATORS IN A NONFLAT COMPLEX SPACE FORM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 21 October 2009, pp. 260-273
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Characterizing warped-product Lagrangian immersions in complex projective space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 2 / June 2009
- Published online by Cambridge University Press:
- 28 May 2009, pp. 273-286
-
- Article
-
- You have access
- Export citation