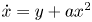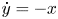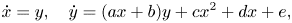Refine listing
Actions for selected content:
32 results in 37Gxx
The cyclicity of the period annulus of a reversible quadratic system
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 10 February 2021, pp. 281-290
- Print publication:
- April 2022
-
- Article
- Export citation
On the birth and death of algebraic limit cycles in quadratic differential systems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 26 May 2020, pp. 317-336
-
- Article
- Export citation
Phase portraits of the quadratic polynomial Liénard differential systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 04 March 2020, pp. 202-216
- Print publication:
- February 2021
-
- Article
- Export citation
Two components is too simple: an example of oscillatory Fisher–KPP system with three components
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 24 September 2019, pp. 3097-3120
- Print publication:
- December 2020
-
- Article
- Export citation
Parametric rigidity of real families of conformal diffeomorphisms tangent to x→−x
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 August 2018, pp. 261-277
- Print publication:
- February 2019
-
- Article
- Export citation
Integrable zero-Hopf singularities and three-dimensional centres
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 17 October 2017, pp. 327-340
- Print publication:
- April 2018
-
- Article
- Export citation
SINGULAR COTANGENT MODEL
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 415-430
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
HOPF BIFURCATION ANALYSIS FOR A RATIO-DEPENDENT PREDATOR–PREY SYSTEM INVOLVING TWO DELAYS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 3 / January 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 214-231
-
- Article
-
- You have access
- Export citation
DYNAMICAL SYSTEMS ANALYSIS OF A MODEL DESCRIBING TASMANIAN DEVIL FACIAL TUMOUR DISEASE
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 54 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 18 March 2013, pp. 89-107
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF LIMIT CYCLES IN PERTURBATIONS OF A QUADRATIC REVERSIBLE CENTER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 409-423
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
The SIS Great Circle Epidemic Model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 513-530
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
Stochastic and deterministic analysis of SIS household epidemics
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 38 / Issue 4 / December 2006
- Published online by Cambridge University Press:
- 08 September 2016, pp. 943-968
- Print publication:
- December 2006
-
- Article
-
- You have access
- Export citation