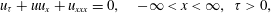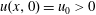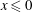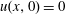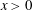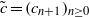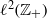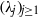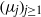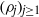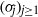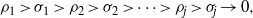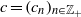Refine listing
Actions for selected content:
42 results in 37Kxx
SPATIAL HAMILTONIAN IDENTITIES FOR NONLOCALLY COUPLED SYSTEMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 14 November 2018, e22
-
- Article
-
- You have access
- Open access
- Export citation
π-TYPE FERMIONS AND π-TYPE KP HIERARCHY
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 14 September 2018, pp. 601-613
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Novel Conformal Structure-Preserving Algorithms for Coupled Damped Nonlinear Schrödinger System
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 28 November 2017, pp. 1383-1403
- Print publication:
- December 2017
-
- Article
- Export citation
Integrable Properties of a Variant of the Discrete Hungry Toda Equations and Their Relationship to Eigenpairs of Band Matrices
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 785-798
- Print publication:
- November 2017
-
- Article
- Export citation
STABILITY THEORY AND HAMILTONIAN DYNAMICS IN THE EULER IDEAL FLUID EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 28 September 2017, pp. 523-524
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Stability of line solitons for the KP-II equation in ℝ2. II
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 September 2017, pp. 149-198
- Print publication:
- February 2018
-
- Article
- Export citation
DISCRETE LINEAR WEINGARTEN SURFACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 55-88
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
A Compact Scheme for Coupled Stochastic Nonlinear Schrödinger Equations
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 21 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 05 December 2016, pp. 93-125
- Print publication:
- January 2017
-
- Article
- Export citation
Exponentially accurate Hamiltonian embeddings of symplectic A-stable Runge–Kutta methods for Hamiltonian semilinear evolution equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 6 / December 2016
- Published online by Cambridge University Press:
- 25 October 2016, pp. 1265-1301
- Print publication:
- December 2016
-
- Article
- Export citation
Integrable Couplings of the Boiti-Pempinelli-Tu Hierarchy and Their Hamiltonian Structures
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 8 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 27 May 2016, pp. 588-598
- Print publication:
- August 2016
-
- Article
- Export citation
Novel Symplectic Discrete Singular Convolution Method for Hamiltonian PDEs
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1375-1396
- Print publication:
- May 2016
-
- Article
- Export citation
On the loss of compactness in the vectorial heteroclinic connection problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 22 March 2016, pp. 595-608
- Print publication:
- June 2016
-
- Article
- Export citation
The Hamiltonian Field Theory of the Von Mises Wave Equation: Analytical and Computational Issues
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 758-769
- Print publication:
- March 2016
-
- Article
- Export citation
Semiclassical orthogonal polynomial systems on nonuniform lattices, deformations of the Askey table, and analogues of isomonodromy
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 127-234
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
SUB-RIEMANNIAN STRUCTURES ON GROUPS OF DIFFEOMORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 4 / September 2017
- Published online by Cambridge University Press:
- 10 August 2015, pp. 745-785
- Print publication:
- September 2017
-
- Article
- Export citation
Bespoke finite difference schemes that preserve multiple conservation laws
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 May 2015, pp. 372-403
-
- Article
-
- You have access
- Export citation
THE LARGE-TIME DEVELOPMENT OF THE SOLUTION TO AN INITIAL-VALUE PROBLEM FOR THE KORTEWEG–DE VRIES EQUATION. II. INITIAL DATA HAS A DISCONTINUOUS COMPRESSIVE STEP
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 14 May 2014, pp. 391-414
- Print publication:
- July 2014
-
- Article
- Export citation
Inverse spectral problems for compact Hankel operators
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 18 April 2013, pp. 273-301
- Print publication:
- April 2014
-
- Article
- Export citation
FOURIER ANALYSIS AND THE KINETIC THEORY OF GASES
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 16 December 2011, pp. 93-208
- Print publication:
- January 2012
-
- Article
- Export citation
Abelian functions associated with genus three algebraic curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 November 2011, pp. 291-326
-
- Article
-
- You have access
- Export citation
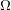
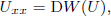
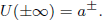
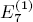 q-Painlevé system.
q-Painlevé system.