Refine listing
Actions for selected content:
31 results in 12Jxx
A Generalization of the Eisenstein–Dumas–Schönemann Irreducibility Criterion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2017, pp. 937-945
-
- Article
- Export citation
Defining Coarsenings of Valuations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 10 January 2017, pp. 665-687
-
- Article
- Export citation
A DEFINABLE
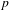 $p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
$p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 20 October 2015, pp. 39-57
- Print publication:
- February 2018
-
- Article
- Export citation
Complexity of OM factorizations of polynomials over local fields
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 16 / October 2013
- Published online by Cambridge University Press:
- 01 June 2013, pp. 139-171
-
- Article
-
- You have access
- Export citation
Orderings and signatures of higher level on multirings and hyperfields
- Part of
-
- Journal:
- Journal of K-Theory / Volume 10 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 16 May 2012, pp. 489-518
- Print publication:
- December 2012
-
- Article
- Export citation
The Ultrametric Corona Problem and spherically complete fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 53 / Issue 2 / June 2010
- Published online by Cambridge University Press:
- 30 April 2010, pp. 353-371
-
- Article
-
- You have access
- Export citation
On Construction of Saturated Distinguished Chains
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 59-65
- Print publication:
- December 2007
-
- Article
- Export citation
On minimal pairs and residually transcendental extensions of valuations
- Part of
-
- Journal:
- Mathematika / Volume 49 / Issue 1-2 / June 2002
- Published online by Cambridge University Press:
- 26 February 2010, pp. 93-106
- Print publication:
- June 2002
-
- Article
- Export citation
A generalized fundamental principle
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 83-92
- Print publication:
- June 1999
-
- Article
- Export citation
The locally convex topology on the space of meromorphic functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-303
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
Value groups and simple transcendental extensions
- Part of
-
- Journal:
- Mathematika / Volume 38 / Issue 2 / December 1991
- Published online by Cambridge University Press:
- 26 February 2010, pp. 381-385
- Print publication:
- December 1991
-
- Article
- Export citation
 -definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.
-definable (non-trivial) Henselian valuations. We then draw some Galois-theoretic conclusions from our results.
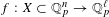
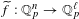
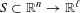
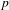
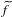
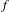
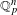
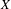
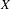
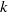

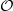
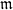
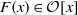

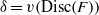

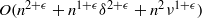
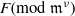
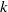
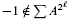 to the full subcategory of ℓ-real reduced multirings, and provide an elementary first-order description of these objects. The relationship between ℓ-real reduced hyperfields and the spaces of signatures defined by Mulcahy and Powers is also examined.
to the full subcategory of ℓ-real reduced multirings, and provide an elementary first-order description of these objects. The relationship between ℓ-real reduced hyperfields and the spaces of signatures defined by Mulcahy and Powers is also examined.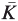 of
of 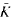 of
of 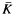 of
of