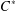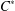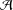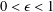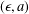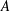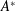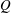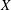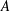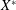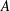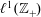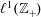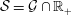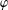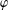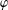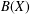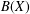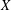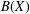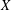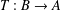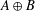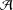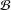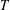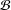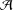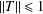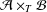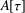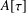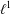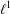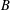Refine listing
Actions for selected content:
97 results in 46Hxx
ARENS PRODUCTS, ARENS REGULARITY AND RELATED PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 04 December 2019, pp. 138-150
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
WEIGHTED CORE–EP INVERSE AND WEIGHTED CORE–EP PRE-ORDERS IN A
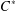 $C^{\ast }$-ALGEBRA
$C^{\ast }$-ALGEBRA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 18 October 2019, pp. 76-110
- Print publication:
- August 2021
-
- Article
- Export citation
CONTINUITY OF A CONDITION SPECTRUM AND ITS LEVEL SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 09 September 2019, pp. 412-430
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Point derivations and cohomologies of Lipschitz algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 18 July 2019, pp. 1173-1187
-
- Article
- Export citation
ESSENTIAL AMENABILITY OF DUAL BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 24 May 2019, pp. 479-488
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Fourier Spaces and Completely Isometric Representations of Arens Product Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 717-747
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Simplicial (Co)-homology of
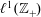 $\ell ^{1}(\mathbb{Z}_{+})$
$\ell ^{1}(\mathbb{Z}_{+})$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 17 December 2018, pp. 756-766
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
r-FREDHOLM THEORY IN BANACH ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 25 September 2018, pp. 615-627
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
A Trace Formula for the Index of B-Fredholm Operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1063-1068
-
- Article
- Export citation
Maximal Ideals in Some Spaces of Bounded Linear Operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 01 February 2018, pp. 251-264
-
- Article
- Export citation
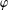 $\unicode[STIX]{x1D711}$ -CONTRACTIBILITY AND
$\unicode[STIX]{x1D711}$ -CONTRACTIBILITY AND 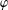 $\unicode[STIX]{x1D711}$ -CONNES AMENABILITY COINCIDE WITH SOME OLDER NOTIONS
$\unicode[STIX]{x1D711}$ -CONNES AMENABILITY COINCIDE WITH SOME OLDER NOTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 30 January 2018, pp. 274-278
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
THE NON-COMMUTATIVE SCHWARTZ SPACE IS WEAKLY AMENABLE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 437-443
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
MORE ON THE ARENS REGULARITY OF
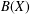 $B(X)$
$B(X)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 296-303
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
TRIVIALITY OF THE GENERALISED LAU PRODUCT ASSOCIATED TO A BANACH ALGEBRA HOMOMORPHISM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 01 March 2016, pp. 286-289
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Orthogonally Additive Polynomials and Orthosymmetric Maps in Banach Algebras with Properties 𝔸 and 𝔹
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 15 December 2015, pp. 559-568
-
- Article
- Export citation
SECOND-ORDER NONCOMMUTATIVE DIFFERENTIAL AND LIPSCHITZ STRUCTURES DEFINED BY A CLOSED SYMMETRIC OPERATOR
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 25 November 2015, pp. 145-162
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
A CHARACTERISATION OF 3-JORDAN HOMOMORPHISMS ON BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 04 September 2015, pp. 301-306
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
A NOTE ON CYCLIC AMENABILITY OF THE LAU PRODUCT OF BANACH ALGEBRAS DEFINED BY A BANACH ALGEBRA MORPHISM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 282-289
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
DERIVATIONS OF FRÉCHET NUCLEAR GB
 $^{\ast }$-ALGEBRAS
$^{\ast }$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 04 June 2015, pp. 290-301
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
HOMOMORPHISMS OF
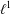 $\ell ^{1}$-MUNN ALGEBRAS AND APPLICATIONS TO SEMIGROUP ALGEBRAS
$\ell ^{1}$-MUNN ALGEBRAS AND APPLICATIONS TO SEMIGROUP ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 02 April 2015, pp. 115-122
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation