Refine listing
Actions for selected content:
32 results in 46Nxx
Nash equilibrium in nonzero-sum games of optimal stopping for Brownian motion
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 49 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 26 June 2017, pp. 430-445
- Print publication:
- June 2017
-
- Article
- Export citation
SPECTRAL ZETA FUNCTIONS FOR THE QUANTUM RABI MODELS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 229 / March 2018
- Published online by Cambridge University Press:
- 01 December 2016, pp. 52-98
- Print publication:
- March 2018
-
- Article
-
- You have access
- HTML
- Export citation
Some Remarks on Davie’s Uniqueness Theorem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 1019-1035
-
- Article
- Export citation
Generalized Lagrange multiplier rule for non-convex vector optimization problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 297-308
- Print publication:
- April 2016
-
- Article
- Export citation
DYADIC SHIFT RANDOMIZATION IN CLASSICAL DISCREPANCY THEORY
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 06 May 2015, pp. 183-209
- Print publication:
- 2016
-
- Article
- Export citation
L1-SMOOTHING FOR THE ORNSTEIN–UHLENBECK SEMIGROUP
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 160-168
- Print publication:
- January 2013
-
- Article
- Export citation
Limit of the Transport Capacity of a Dense Wireless Network
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 47 / Issue 3 / September 2010
- Published online by Cambridge University Press:
- 14 July 2016, pp. 886-892
- Print publication:
- September 2010
-
- Article
-
- You have access
- Export citation
On the Almost Sure Central Limit Theorem for Vector Martingales: Convergence of Moments and Statistical Applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 46 / Issue 1 / March 2009
- Published online by Cambridge University Press:
- 14 July 2016, pp. 151-169
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Pricing of Catastrophe Insurance Options Under Immediate Loss Reestimation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 831-845
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
Two Remarks on Blackwell's Theorem
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 580-586
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
On Utility-Based Superreplication Prices of Contingent Claims with Unbounded Payoffs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 44 / Issue 4 / December 2007
- Published online by Cambridge University Press:
- 14 July 2016, pp. 880-888
- Print publication:
- December 2007
-
- Article
-
- You have access
- Export citation
Stable perturbation in Banach algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 271-284
- Print publication:
- October 2007
-
- Article
-
- You have access
- Export citation
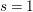

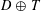
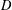
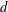
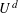
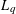
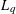
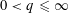
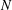
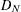
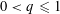
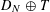
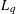
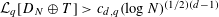
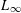
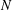
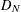
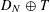
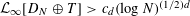
 be a unital Banach algebra. Assume that a has
be a unital Banach algebra. Assume that a has 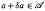 is said to be a stable perturbation of a if
is said to be a stable perturbation of a if 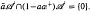 . In this paper we give various conditions for stable perturbation of a generalized invertible element and show that the equation
. In this paper we give various conditions for stable perturbation of a generalized invertible element and show that the equation 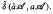 . These results will be applied to error estimates for perturbations of the Moore-Penrose inverse in C*–algebras and the Drazin inverse in Banach algebras.
. These results will be applied to error estimates for perturbations of the Moore-Penrose inverse in C*–algebras and the Drazin inverse in Banach algebras.