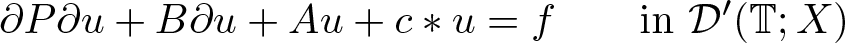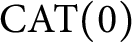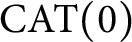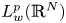Refine listing
Actions for selected content:
32 results in 46Nxx
Density and unitarity of the Burau representation from a non-semisimple TQFT
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-29
-
- Article
- Export citation
The invariant subspaces of periodic Fourier multipliers with application to abstract evolution equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1-47
-
- Article
- Export citation
Generalized Knill–Laflamme theorem for families of isoclinic subspaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 992-1010
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complete positivity order and relative entropy decay
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 06 February 2025, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a class of bivariate distributions built of q-ultraspherical polynomials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 02 December 2024, pp. 1-34
-
- Article
- Export citation
Pressure of a dilute spin-polarized Fermi gas: Lower bound
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Co-spectral radius for countable equivalence relations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 3385-3427
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coupling capacity in C*-algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 September 2023, pp. 81-103
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Uncertainty principles in holomorphic function spaces on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 122-136
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new lifetime distribution by maximizing entropy: properties and applications
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 February 2023, pp. 189-206
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new second-order upper bound for the ground state energy of dilute Bose gases
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 18 November 2021, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Direction-dependent turning leads to anisotropic diffusion and persistence
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 4 / August 2022
- Published online by Cambridge University Press:
- 23 June 2021, pp. 729-765
-
- Article
- Export citation
Self-adjoint extensions of bipartite Hamiltonians
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 22 June 2021, pp. 433-447
-
- Article
- Export citation
REFLEXIVITY INDEX AND IRRATIONAL ROTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 29 March 2021, pp. 493-505
- Print publication:
- December 2021
-
- Article
- Export citation
A note on Mosco convergence in
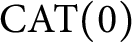 $\operatorname {\mathrm {CAT}}(0)$ spaces
$\operatorname {\mathrm {CAT}}(0)$ spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 17 January 2021, pp. 994-1003
- Print publication:
- December 2022
-
- Article
- Export citation
On decay rates of the solutions of parabolic Cauchy problems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 21 July 2020, pp. 1021-1039
- Print publication:
- June 2021
-
- Article
- Export citation
A non-exponential extension of Sanov’s theorem via convex duality
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 52 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 29 April 2020, pp. 61-101
- Print publication:
- March 2020
-
- Article
- Export citation
SURVEY: SIXTY YEARS OF DOUGLAS–RACHFORD
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 333-370
- Print publication:
- June 2021
-
- Article
- Export citation
Exponential models by Orlicz spaces and applications
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 682-700
- Print publication:
- September 2018
-
- Article
- Export citation
FUNCTIONAL VERSIONS OF SOME REFINED AND REVERSED OPERATOR MEAN INEQUALITIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 10 August 2017, pp. 496-503
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation