Refine listing
Actions for selected content:
36 results in 54Bxx
CARDINALITY OF INVERSE LIMITS WITH UPPER SEMICONTINUOUS BONDING FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 23 September 2014, pp. 167-174
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
A DUALIZING OBJECT APPROACH TO NONCOMMUTATIVE STONE DUALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 19 August 2013, pp. 383-403
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
On the classification of the real vector subspaces of a quaternionic vector space
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 03 April 2013, pp. 615-622
-
- Article
-
- You have access
- Export citation
INVERSE LIMITS IN THE CATEGORY OF COMPACT HAUSDORFF SPACES AND UPPER SEMICONTINUOUS FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 22 March 2013, pp. 49-59
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
THE BAIRE PROPERTY IN THE REMAINDERS OF SEMITOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 21 January 2013, pp. 301-308
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
PRODUCTS OF BASE-κ-PARACOMPACT SPACES AND COMPACT SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 21 July 2011, pp. 387-392
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Mutually Aposyndetic Decomposition of Homogeneous Continua: Dedicated to Charles L. Hagopian and James T. Rogers
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 182-201
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
Products of Weak P-Spaces and K-Analytic Spaces
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 67-81
- Print publication:
- December 2007
-
- Article
- Export citation
Manifolds that fail to be co-dimension 2 fibrators necessarily cover themselves
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 1 / February 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 61-68
- Print publication:
- February 2003
-
- Article
-
- You have access
- Export citation
Functional equations in total negation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 334-339
- Print publication:
- June 2000
-
- Article
-
- You have access
- Export citation
Infima of hyperspace topologies
- Part of
-
- Journal:
- Mathematika / Volume 42 / Issue 1 / June 1995
- Published online by Cambridge University Press:
- 26 February 2010, pp. 67-86
- Print publication:
- June 1995
-
- Article
- Export citation
Countable unions of compact spaces with the Namioka property
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-144
- Print publication:
- June 1994
-
- Article
- Export citation
A generalization of Tong's theorem and properties of pairwise perfectly normal spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 3 / December 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 353-359
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
Monoidal closed structures on categories with constant maps
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 175-185
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
Maps on D1 and D2 spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 106-109
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
The Lindelöf degree of scattered spaces and their products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 98-105
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
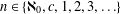

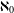

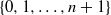
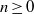
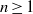
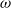
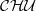
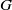
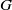
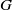
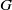
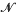 *, if, for every Baire space
*, if, for every Baire space 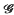
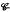 binary relations.
binary relations.