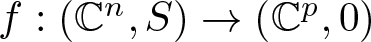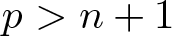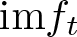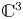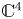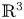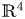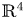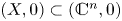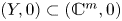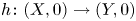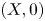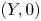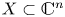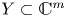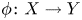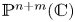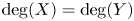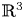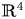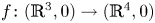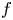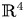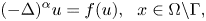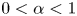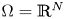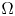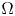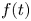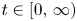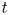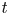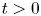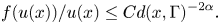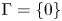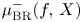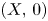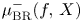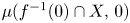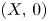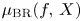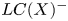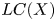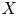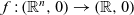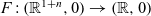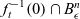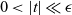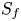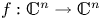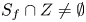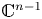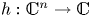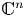Refine listing
Actions for selected content:
31 results in 58Kxx
Double points and image of reflection maps
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 December 2025, pp. 1-45
-
- Article
- Export citation
On the non-properness set of a local homeomorphism
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 30 September 2025, pp. 1-15
-
- Article
- Export citation
Isotypical components of the homology of ICIS and images of deformations of map germs
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 February 2025, pp. 1-40
-
- Article
- Export citation
Global index of real polynomials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 18 March 2024, pp. 2020-2048
- Print publication:
- December 2025
-
- Article
- Export citation
Deformations of corank 1 frontals
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1204-1234
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On k-folding map-germs and hidden symmetries of surfaces in the Euclidean 3-space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 26 January 2023, pp. 60-104
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Singularities of 3-parameter line congruences in $\mathbb {R}^{4}$
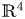
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 1045-1070
- Print publication:
- June 2023
-
- Article
- Export citation
On the Fukui–Kurdyka–Paunescu conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 11 August 2022, pp. 1298-1313
- Print publication:
- June 2022
-
- Article
- Export citation
The dual tree of a fold map germ from $\mathbb {R}^{3}$
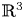 to $\mathbb {R}^{4}$
to $\mathbb {R}^{4}$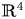
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 May 2022, pp. 958-977
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Qualitative properties of singular solutions to fractional elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 14 September 2021, pp. 1155-1190
- Print publication:
- October 2022
-
- Article
- Export citation
The relative Bruce–Roberts number of a function on a hypersurface
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 19 August 2021, pp. 662-674
-
- Article
- Export citation
TOPOLOGY OF 1-PARAMETER DEFORMATIONS OF NON-ISOLATED REAL SINGULARITIES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 30 July 2021, pp. 484-498
- Print publication:
- May 2022
-
- Article
- Export citation
NOTES ON VANISHING CYCLES AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 29 October 2020, pp. 371-415
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Envelopes of families of framed surfaces and singular solutions of first-order partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 15 September 2020, pp. 1515-1542
- Print publication:
- October 2021
-
- Article
- Export citation
On topological approaches to the Jacobian conjecture in ℂn
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 666-675
-
- Article
- Export citation
Kato–Matsumoto-type results for disentanglements
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1-27
- Print publication:
- February 2021
-
- Article
-
- You have access
- Open access
- Export citation
Global Euler obstruction, global Brasselet numbers and critical points
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 14 May 2019, pp. 2503-2534
- Print publication:
- October 2020
-
- Article
- Export citation
Frame and direction mappings for surfaces in ℝ3
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 26 January 2019, pp. 795-830
- Print publication:
- June 2019
-
- Article
- Export citation
Evolutes and focal surfaces of framed immersions in the Euclidean space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 497-516
- Print publication:
- February 2020
-
- Article
- Export citation
Galois theory for general systems of polynomial equations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 229-245
- Print publication:
- February 2019
-
- Article
- Export citation