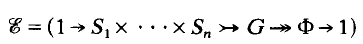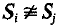Refine listing
Actions for selected content:
545 results in 20Fxx
On surface Bieberbach groups
- Part of
-
- Journal:
- Mathematika / Volume 34 / Issue 1 / June 1987
- Published online by Cambridge University Press:
- 26 February 2010, pp. 82-85
- Print publication:
- June 1987
-
- Article
- Export citation
CLT groups and wreath products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-195
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
Semidirect product groups with Abelian automorphism groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 1 / February 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 84-91
- Print publication:
- February 1987
-
- Article
-
- You have access
- Export citation
A class of finite groups having nilpotent injectors
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 361-365
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Products of locally finite groups with min-p
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 352-360
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
2-groups with every automorphism central
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 2 / October 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 233-236
- Print publication:
- October 1986
-
- Article
-
- You have access
- Export citation
Automorphism orbits of finite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-260
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
Automorphisms of nilpotent groups of class two with small rank
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 1 / August 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 121-131
- Print publication:
- August 1985
-
- Article
-
- You have access
- Export citation
Some finite groups with few defining relations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 230-240
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
Quotient closed metanilpotent Fitting classes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 157-163
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
Some examples of finiteness conditions in centre-by-metabelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 2 / April 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 171-174
- Print publication:
- April 1985
-
- Article
-
- You have access
- Export citation
On the lower central factors of free centre-by-metabelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 1 / February 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 65-75
- Print publication:
- February 1985
-
- Article
-
- You have access
- Export citation
Epimorphisms preserving perfect radicals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-364
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
A conjecture of Lennox and Wiegold concerning supersoluble groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 35 / Issue 2 / October 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 218-220
- Print publication:
- October 1983
-
- Article
-
- You have access
- Export citation
Groups sharing some varietal properties with supersoluble groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 2 / April 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 265-268
- Print publication:
- April 1983
-
- Article
-
- You have access
- Export citation
Finite varieties and groups with Sylow p-subgroups of low class
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 464-469
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
Extensions of a problem of Paul Erdös on groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 4 / December 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 459-463
- Print publication:
- December 1981
-
- Article
-
- You have access
- Export citation
On the Schur-Baer property
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 3 / October 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 343-361
- Print publication:
- October 1981
-
- Article
-
- You have access
- Export citation
A characterization of finite p-soluble groups of p-length one by commutator identities
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 3 / February 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-263
- Print publication:
- February 1981
-
- Article
-
- You have access
- Export citation
Some cancellation theorems
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 30 / Issue 1 / September 1980
- Published online by Cambridge University Press:
- 09 April 2009, pp. 87-97
- Print publication:
- September 1980
-
- Article
-
- You have access
- Export citation