Refine listing
Actions for selected content:
545 results in 20Fxx
Torsion-free groups isomorphic to all of their non-nilpotent subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 339-348
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Modules over infinite nilpotent groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 211-222
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
On a family of cyclically-presented fundamental groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 235-242
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
On (2, 3, 7)-generation of maximal parabolic subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-200
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation
Towers, ladders and the B. B. Newman Spelling Theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 53-69
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
A problem of expressibility in some amalgamated products of groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 105-115
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Remarks concerning finitely generated semigroups having regular sets of unique normal forms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 293-310
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
On profinite groups in which commutators are Engel
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-9
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
On real forms of a complex algebraic curve
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 134-142
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
m-Wielandt series in infinite groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 1 / February 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 76-87
- Print publication:
- February 2001
-
- Article
-
- You have access
- Export citation
The order of groups satisfying a converse to Lagrange's theorem
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 197-204
- Print publication:
- December 2000
-
- Article
- Export citation
Locally graded groups with a nilpotency condition on infinite subsets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 415-420
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
On the homotopy type of the p-subgroup complex for finite solvable groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 212-228
- Print publication:
- October 2000
-
- Article
-
- You have access
- Export citation
Tameness and geodesic cores of subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 2 / October 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 153-161
- Print publication:
- October 2000
-
- Article
-
- You have access
- Export citation
Diagrammatically reducible complexes and Haken manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 116-126
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
Some Properties on Isologism of Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 1 / February 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-9
- Print publication:
- February 2000
-
- Article
-
- You have access
- Export citation
Soluble groups isomorphic to their non-nilpotent subgroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 3 / December 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 399-411
- Print publication:
- December 1999
-
- Article
-
- You have access
- Export citation
Finitely generated residually torsion-free nilpotent groups. I
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 3 / December 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-317
- Print publication:
- December 1999
-
- Article
-
- You have access
- Export citation
A group with very strange decomposition properties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 185-190
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
Computation of nilpotent engel groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 214-222
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
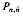 of
of 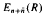 consisting of the matrices of shape
consisting of the matrices of shape 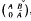 , where
, where 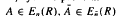 and
and 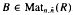 , is (2, 3, 7)-generated whenever
, is (2, 3, 7)-generated whenever 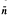 are large enough.
are large enough.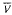 (
(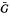 =
= 