Refine listing
Actions for selected content:
545 results in 20Fxx
Infinite presentability of groups and condensation
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 811-848
- Print publication:
- October 2014
-
- Article
- Export citation
LOCALLY FINITE GROUPS WHOSE SUBGROUPS HAVE FINITE NORMAL OSCILLATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 20 November 2013, pp. 479-487
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Braid group actions via categorifiedHeisenberg complexes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 09 October 2013, pp. 105-142
- Print publication:
- January 2014
-
- Article
- Export citation
CANNON–THURSTON MAPS DO NOT ALWAYS EXIST
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 11 September 2013, e3
-
- Article
-
- You have access
- Open access
- Export citation
CONCISENESS OF COPRIME COMMUTATORS IN FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 252-258
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
MINIMAL VOLUME OF COMPLETE UNIFORM VISIBILITY MANIFOLDS WITH FINITE VOLUME
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 375-384
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Proper isometric actions of hyperbolic groups on
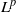 $L^p$-spaces
$L^p$-spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 5 / May 2013
- Published online by Cambridge University Press:
- 26 February 2013, pp. 773-792
- Print publication:
- May 2013
-
- Article
- Export citation
The string of nets
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 05 December 2012, pp. 223-262
-
- Article
-
- You have access
- Export citation
PyCox: computing with (finite) Coxeter groups and Iwahori–Hecke algebras
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 August 2012, pp. 231-256
-
- Article
-
- You have access
- Export citation
FINITELY GENERATED SOLUBLE GROUPS WITH A CONDITION ON INFINITE SUBSETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 13 June 2012, pp. 152-157
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
Groups acting simply transitively on vertex sets of hyperbolic triangular buildings
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 May 2012, pp. 101-112
-
- Article
-
- You have access
- Export citation
Testing commutativity of a group and the power of randomization
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 April 2012, pp. 38-43
-
- Article
-
- You have access
- Export citation
Invariants of reflection groups, arrangements, and normality of decomposition classes in Lie algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 921-930
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
COHOMOLOGY AND PROFINITE TOPOLOGIES FOR SOLVABLE GROUPS OF FINITE RANK
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 254-265
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
Proof of Cellini’s conjecture on self-avoiding paths in Coxeter groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 548-554
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
Poincaré inequalities, embeddings, and wild groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 24 August 2011, pp. 1546-1572
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Actions of higher-rank lattices on free groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 5 / September 2011
- Published online by Cambridge University Press:
- 29 July 2011, pp. 1573-1580
- Print publication:
- September 2011
-
- Article
-
- You have access
- Export citation
Symmetric presentations of Coxeter groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 20 June 2011, pp. 669-683
-
- Article
-
- You have access
- Export citation
A NOTE ON NIELSEN EQUIVALENCE IN FINITELY GENERATED ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 16 June 2011, pp. 127-136
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
ON VERBAL SUBGROUPS IN RESIDUALLY FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 10 June 2011, pp. 159-170
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
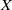
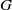
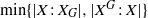
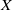
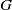

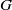
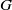
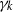
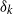
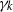
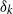
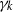
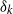
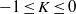
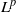
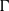
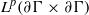
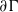
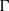
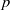
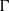
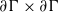
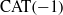
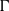
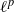
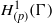
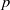
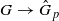 induces an isomorphism
induces an isomorphism 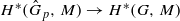 for any discrete
for any discrete 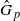 -module
-module 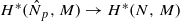 is an isomorphism for any discrete
is an isomorphism for any discrete 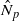 -module
-module 