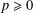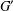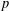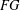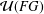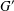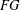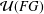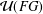Refine listing
Actions for selected content:
545 results in 20Fxx
POLYCYCLIC, METABELIAN OR SOLUBLE OF TYPE (FP)∞ GROUPS WITH BOOLEAN ALGEBRA OF RATIONAL SETS AND BIAUTOMATIC SOLUBLE GROUPS ARE VIRTUALLY ABELIAN
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 13 March 2017, pp. 209-218
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
Coarse flow spaces for relatively hyperbolic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 09 March 2017, pp. 745-779
- Print publication:
- April 2017
-
- Article
- Export citation
ASYMPTOTIC TRIANGULATIONS AND COXETER TRANSFORMATIONS OF THE ANNULUS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 27 February 2017, pp. 63-96
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
On the Universal SL2-Representation Rings of Free Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 30 January 2017, pp. 973-1001
-
- Article
- Export citation
On the Asphericity of a Family of Positive Relative Group Presentations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 05 January 2017, pp. 545-564
-
- Article
- Export citation
SYMMETRIC CROSSCAP NUMBER OF GROUPS OF ORDER LESS THAN OR EQUAL TO 63
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 23 December 2016, pp. 145-156
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
On Groups with Slow Intersection Growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 14 November 2016, pp. 387-390
-
- Article
- Export citation
NILPOTENCY IN UNCOUNTABLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 27 October 2016, pp. 59-69
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Ramification conjecture and Hirzebruch’s property of line arrangements
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 12 / December 2016
- Published online by Cambridge University Press:
- 25 October 2016, pp. 2443-2460
- Print publication:
- December 2016
-
- Article
- Export citation
THE
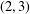 $(2,3)$ -GENERATION OF THE SPECIAL LINEAR GROUPS OVER FINITE FIELDS
$(2,3)$ -GENERATION OF THE SPECIAL LINEAR GROUPS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 26 September 2016, pp. 48-53
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
QUASIRANDOM GROUP ACTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 30 August 2016, e24
-
- Article
-
- You have access
- Open access
- Export citation
ENGEL RELATIONS IN 4-MANIFOLD TOPOLOGY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 16 August 2016, e22
-
- Article
-
- You have access
- Open access
- Export citation
Whitney regularity of the image of the Chevalley mapping
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 13 July 2016, pp. 895-904
- Print publication:
- October 2016
-
- Article
- Export citation
GROWTHS OF ENDOMORPHISMS OF FINITELY GENERATED SEMIGROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 08 July 2016, pp. 163-184
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
Finite Groups and Lie Rings with an Automorphism of Order 2n
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 15 June 2016, pp. 391-412
-
- Article
- Export citation
ABELIAN AND METABELIAN QUOTIENT GROUPS OF SURFACE BRAID GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 119-142
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
LOCAL REPRESENTATIONS OF THE LOOP BRAID GROUP
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 359-378
- Print publication:
- May 2017
-
- Article
-
- You have access
- Export citation
EQUIVARIANT COMPRESSION OF CERTAIN DIRECT LIMIT GROUPS AND AMALGAMATED FREE PRODUCTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 10 June 2016, pp. 739-752
- Print publication:
- September 2016
-
- Article
-
- You have access
- Export citation
GROUP ALGEBRAS WITH ENGEL UNIT GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 101 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 March 2016, pp. 244-252
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
THE FIRST-ORDER THEORY OF BRANCH GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 February 2016, pp. 150-158
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
 for
for 
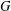
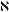
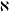
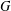
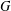
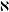
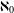
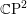
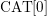
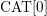
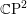
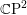
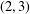
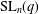
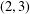
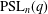

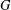
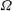
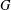
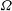
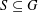
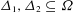
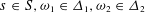
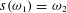

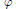 of order 2
of order 2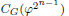 of the involution
of the involution 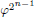 is nilpotent of class
is nilpotent of class 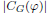 ) be the number of fixed points of
) be the number of fixed points of