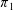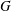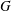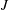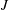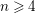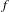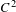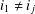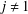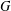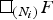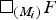Refine listing
Actions for selected content:
544 results in 20Fxx
Non-cocompact Group Actions and
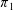 $\unicode[STIX]{x1D70B}_{1}$-Semistability at Infinity
$\unicode[STIX]{x1D70B}_{1}$-Semistability at Infinity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 26 June 2019, pp. 1275-1303
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Recurrence of quadratic differentials for harmonic measure
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 25 June 2019, pp. 299-305
- Print publication:
- September 2020
-
- Article
- Export citation
ON THE RECOGNITION OF RIGHT-ANGLED ARTIN GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 19 June 2019, pp. 473-475
- Print publication:
- May 2020
-
- Article
-
- You have access
- Export citation
Linear syzygies, hyperbolic Coxeter groups and regularity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 20 May 2019, pp. 1076-1097
- Print publication:
- June 2019
-
- Article
- Export citation
EXCHANGE MOVES AND NONCONJUGATE BRAID REPRESENTATIVES OF KNOTS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 20 May 2019, pp. 298-321
- Print publication:
- December 2020
-
- Article
-
- You have access
- HTML
- Export citation
JSJ DECOMPOSITIONS OF DOUBLES OF FREE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 02 May 2019, pp. 367-382
- Print publication:
- May 2020
-
- Article
-
- You have access
- Open access
- Export citation
Embedding right-angled Artin groups into Brin–Thompson groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 23 April 2019, pp. 225-229
- Print publication:
- September 2020
-
- Article
- Export citation
Weak containment of measure-preserving group actions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 17 April 2019, pp. 2681-2733
- Print publication:
- October 2020
-
- Article
- Export citation
Profinite groups with restricted centralizers of commutators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 01 April 2019, pp. 2301-2321
- Print publication:
- October 2020
-
- Article
- Export citation
2-chains and square roots of Thompson’s group
 $F$
$F$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2515-2532
- Print publication:
- September 2020
-
- Article
- Export citation
Hyperfiniteness of boundary actions of cubulated hyperbolic groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2453-2466
- Print publication:
- September 2020
-
- Article
- Export citation
A NILPOTENCY CRITERION FOR SOME VERBAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 281-289
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Duality between p-groups with three characteristic subgroups and semisimple anti-commutative algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 25 February 2019, pp. 1827-1852
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
The Conjugacy Ratio of Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 22 February 2019, pp. 895-911
-
- Article
-
- You have access
- Export citation
Linear Groups with Almost Right Engel Elements
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 789-797
-
- Article
- Export citation
Coarse fundamental groups and box spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1139-1154
- Print publication:
- June 2020
-
- Article
- Export citation
The Weak Order on Weyl Posets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 867-899
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
A new test for asphericity and diagrammatic reducibility of group presentations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 871-895
- Print publication:
- April 2020
-
- Article
- Export citation
THE SET OF QUANTUM CORRELATIONS IS NOT CLOSED
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 7 / 2019
- Published online by Cambridge University Press:
- 14 January 2019, e1
-
- Article
-
- You have access
- Open access
- Export citation
On the Weak Order of Coxeter Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 10 January 2019, pp. 299-336
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation