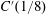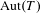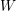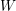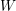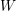Refine listing
Actions for selected content:
544 results in 20Fxx
Geometry of Infinitely Presented Small Cancellation Groups and Quasi-homomorphisms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 997-1018
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Lipschitz 1-connectedness for Some Solvable Lie Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 533-555
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Two-color Soergel Calculus and Simple Transitive 2-representations
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1523-1566
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Mixed Perverse Sheaves on Flag Varieties for Coxeter Groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1-55
- Print publication:
- February 2020
-
- Article
-
- You have access
- Export citation
Casselman’s Basis of Iwahori Vectors and Kazhdan–Lusztig Polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1351-1366
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
LARGE-SCALE SUBLINEARLY LIPSCHITZ GEOMETRY OF HYPERBOLIC SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1831-1876
- Print publication:
- November 2020
-
- Article
- Export citation
Cogrowth for group actions with strongly contracting elements
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1738-1754
- Print publication:
- July 2020
-
- Article
- Export citation
Left Braces and the Quantum Yang–Baxter Equation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 595-608
-
- Article
- Export citation
PRESENTATIONS OF AFFINE KAC–MOODY GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 26 October 2018, e21
-
- Article
-
- You have access
- Open access
- Export citation
COMPLEX OF RELATIVELY HYPERBOLIC GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 09 October 2018, pp. 657-672
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
The HOMFLY-PT polynomials of sublinks and the Yokonuma–Hecke algebras
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 18 September 2018, pp. 1269-1278
- Print publication:
- December 2018
-
- Article
- Export citation
LOCALLY COMPACT WREATH PRODUCTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 26-52
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
CHABAUTY LIMITS OF SIMPLE GROUPS ACTING ON TREES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1093-1120
- Print publication:
- July 2020
-
- Article
- Export citation
CHABAUTY LIMITS OF ALGEBRAIC GROUPS ACTING ON TREES THE QUASI-SPLIT CASE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1031-1091
- Print publication:
- July 2020
-
- Article
- Export citation
ON CANONICAL BASES AND INDUCTION OF
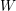 $W$-GRAPHS
$W$-GRAPHS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 17 July 2018, pp. 1-41
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
EXHAUSTION OF THE CURVE GRAPH VIA RIGID EXPANSIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 06 July 2018, pp. 195-230
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
ON PAIRED ROOT SYSTEMS OF COXETER GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 18 June 2018, pp. 347-365
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
Lattice structure of Weyl groups via representation theory of preprojective algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1269-1305
- Print publication:
- June 2018
-
- Article
- Export citation
INTERSECTIONS OF MULTICURVES FROM DYNNIKOV COORDINATES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 149-158
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Diffeomorphism groups of tame Cantor sets and Thompson-like groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1066-1110
- Print publication:
- May 2018
-
- Article
- Export citation