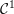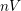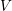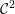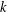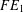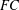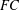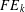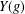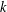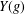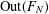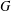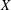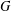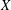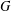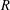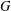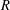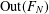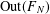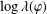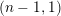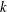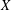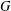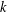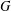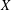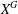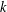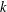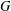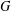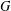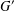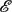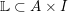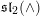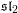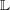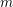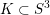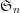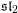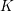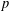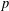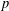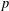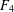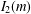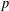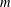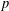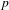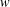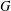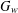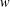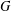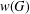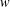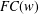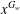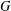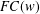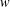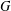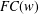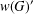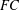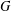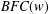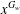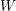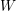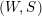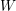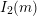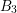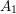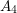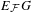Refine listing
Actions for selected content:
545 results in 20Fxx
Diffeomorphism groups of tame Cantor sets and Thompson-like groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1066-1110
- Print publication:
- May 2018
-
- Article
- Export citation
A NILPOTENCY-LIKE CONDITION FOR INFINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 24-33
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
COUNTING CONJUGACY CLASSES IN
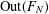 $\text{Out}(F_{N})$
$\text{Out}(F_{N})$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 28 March 2018, pp. 412-421
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
DISTRIBUTION OF ACCUMULATION POINTS OF ROOTS FOR TYPE (n - 1, 1) COXETER GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 235 / September 2019
- Published online by Cambridge University Press:
- 01 March 2018, pp. 127-157
- Print publication:
- September 2019
-
- Article
-
- You have access
- HTML
- Export citation
Free and Properly Discontinuous Actions of Groups on Homotopy 2n-spheres
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 08 February 2018, pp. 305-327
-
- Article
- Export citation
GROUPS OF FINITE NORMAL LENGTH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 01 February 2018, pp. 229-239
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
WEAK CAYLEY TABLE GROUPS OF SOME CRYSTALLOGRAPHIC GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 635-660
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
FINITE GROUPS WITH ENGEL SINKS OF BOUNDED RANK
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 28 January 2018, pp. 695-701
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
Annular Khovanov homology and knotted Schur–Weyl representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 3 / March 2018
- Published online by Cambridge University Press:
- 28 November 2017, pp. 459-502
- Print publication:
- March 2018
-
- Article
- Export citation
ON POWERS OF HALF-TWISTS IN M(0, 2n)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 333-338
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
GRAPH PRODUCTS AND THE ABSENCE OF PROPERTY (AR)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 16 October 2017, pp. 274-288
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
CLASSIFICATION OF REFLECTION SUBGROUPS MINIMALLY CONTAINING
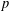 $p$ -SYLOW SUBGROUPS
$p$ -SYLOW SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 57-68
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
EQUIVARIANT GEOMETRY OF BANACH SPACES AND TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 07 September 2017, e22
-
- Article
-
- You have access
- Open access
- Export citation
THE LOWER RANK OF DIRECT PRODUCTS OF HEREDITARILY JUST INFINITE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 04 September 2017, pp. 225-230
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
WHITTAKER FUNCTIONS AND DEMAZURE CHARACTERS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 22 June 2017, pp. 759-781
- Print publication:
- July 2019
-
- Article
- Export citation
ON GROUPS WITH FINITE CONJUGACY CLASSES IN A VERBAL SUBGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 June 2017, pp. 429-437
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
CANNON–THURSTON MAPS FOR KLEINIAN GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 5 / 2017
- Published online by Cambridge University Press:
- 22 May 2017, e1
-
- Article
-
- You have access
- Open access
- Export citation
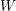 $W$ -GRAPHS AND GYOJA’S
$W$ -GRAPHS AND GYOJA’S 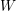 $W$ -GRAPH ALGEBRA
$W$ -GRAPH ALGEBRA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 226 / June 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 1-43
- Print publication:
- June 2017
-
- Article
-
- You have access
- HTML
- Export citation
DISMANTLABLE CLASSIFYING SPACE FOR THE FAMILY OF PARABOLIC SUBGROUPS OF A RELATIVELY HYPERBOLIC GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 2 / March 2019
- Published online by Cambridge University Press:
- 11 April 2017, pp. 329-345
- Print publication:
- March 2019
-
- Article
- Export citation
UNDECIDABILITY AND THE DEVELOPABILITY OF PERMUTOIDS AND RIGID PSEUDOGROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 20 March 2017, e10
-
- Article
-
- You have access
- Open access
- Export citation