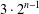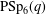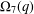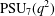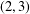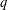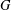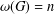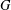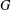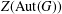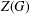Refine listing
Actions for selected content:
545 results in 20Fxx
IMAGES OF QUANTUM REPRESENTATIONS OF MAPPING CLASS GROUPS AND DUPONT–GUICHARDET–WIGNER QUASI-HOMOMORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 27 January 2016, pp. 277-304
- Print publication:
- April 2018
-
- Article
- Export citation
AN ALTERNATE PROOF OF WISE’S MALNORMAL SPECIAL QUOTIENT THEOREM
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 4 / 2016
- Published online by Cambridge University Press:
- 12 January 2016, e1
-
- Article
-
- You have access
- Open access
- Export citation
On locally graded groups with a word whose values are Engel
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 17 December 2015, pp. 533-539
-
- Article
- Export citation
CoxIter – Computing invariants of hyperbolic Coxeter groups
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 754-773
-
- Article
-
- You have access
- Export citation
Geodesics in Trees of Hyperbolic and Relatively Hyperbolic Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 701-740
-
- Article
- Export citation
GROUPS OF INFINITE RANK WITH NORMALITY CONDITIONS ON SUBGROUPS WITH SMALL NORMAL CLOSURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 48-53
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
ON GENERALISED FC-GROUPS IN WHICH NORMALITY IS A TRANSITIVE RELATION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 29 October 2015, pp. 192-198
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
‘ON SETS OF PP-GENERATORS OF FINITE GROUPS’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 05 October 2015, pp. 350-352
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
TRANSVERSALS AS GENERATING SETS IN FINITELY GENERATED GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 19 August 2015, pp. 47-60
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
THE (2,3)-GENERATION OF THE CLASSICAL SIMPLE GROUPS OF DIMENSIONS 6 AND 7
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 05 August 2015, pp. 61-72
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
THE CANCELLATION NORM AND THE GEOMETRY OF BI-INVARIANT WORD METRICS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 153-176
- Print publication:
- January 2016
-
- Article
-
- You have access
- Export citation
ON NONCOMMUTING SETS AND CENTRALISERS IN INFINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 42-46
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
THE SUBGROUP COMMUTATIVITY DEGREE OF FINITE
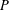 $P$-GROUPS
$P$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 37-41
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
ON THE CENTRE OF THE AUTOMORPHISM GROUP OF A GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 390-396
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
FIXED POINT CHARACTERISATION FOR EXACT AND AMENABLE ACTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 228-232
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
Inversion is Possible in Groups with no Periodic Automorphisms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 05 June 2015, pp. 11-16
-
- Article
- Export citation
Finiteness Properties of Some Groups of Local Similarities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 10 April 2015, pp. 379-402
-
- Article
-
- You have access
- Export citation
Champ: a Cherednik algebra Magma package
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 266-307
-
- Article
-
- You have access
- Export citation
ON GROUPS PRESENTED BY MONADIC REWRITING SYSTEMS WITH GENERATORS OF FINITE ORDER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 06 March 2015, pp. 426-434
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
A Numerical Lower Bound for the Spectral Radius of Random Walks on Surface Groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 24 / Issue 6 / November 2015
- Published online by Cambridge University Press:
- 29 January 2015, pp. 838-856
-
- Article
- Export citation