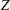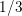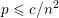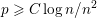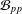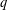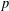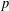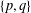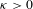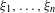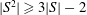Refine listing
Actions for selected content:
545 results in 20Fxx
‘COHOMOLOGY AND PROFINITE TOPOLOGIES FOR SOLVABLE GROUPS OF FINITE RANK’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 12 January 2015, pp. 351-352
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Coherent presentations of Artin monoids
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 957-998
- Print publication:
- May 2015
-
- Article
- Export citation
ON THE CONNECTEDNESS OF THE BRANCH LOCI OF NON-ORIENTABLE UNBORDERED KLEIN SURFACES OF LOW GENUS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 211-230
- Print publication:
- January 2015
-
- Article
-
- You have access
- Export citation
LINEAR AND PROJECTIVE BOUNDARY OF NILPOTENT GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 591-632
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
STRONGLY INVARIANT SUBGROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 431-443
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
CHARACTER TABLES OF METACYCLIC GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 387-400
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
EMBEDDABILITY OF GENERALISED WREATH PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 15 December 2014, pp. 250-263
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
Random triangular groups at density
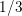 $1/3$
$1/3$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 167-178
- Print publication:
- January 2015
-
- Article
- Export citation
Random groups and nonarchimedean lattices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 16 October 2014, e26
-
- Article
-
- You have access
- Open access
- Export citation
ON SETS OF PP-GENERATORS OF FINITE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 241-249
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
WORDS AND PRONILPOTENT SUBGROUPS IN PROFINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 29 September 2014, pp. 343-364
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
Minimal length elements of extended affine Weyl groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 11 / November 2014
- Published online by Cambridge University Press:
- 19 August 2014, pp. 1903-1927
- Print publication:
- November 2014
-
- Article
- Export citation
NONCOMMUTATIVE REAL ALGEBRAIC GEOMETRY OF KAZHDAN’S PROPERTY (T)
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 15 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 30 July 2014, pp. 85-90
- Print publication:
- January 2016
-
- Article
- Export citation
NONORTHOGONAL GEOMETRIC REALIZATIONS OF COXETER GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 25 July 2014, pp. 180-211
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
FINITELY ANNIHILATED GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 404-417
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A GROUP SUM INEQUALITY AND ITS APPLICATION TO POWER GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 418-426
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
ON A PROBLEM OF P. HALL FOR ENGEL WORDS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 13 May 2014, pp. 237-246
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
SMALL DOUBLING IN ORDERED GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 30 April 2014, pp. 316-325
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
FREE GROUPS AND AUTOMORPHISM GROUPS OF INFINITE STRUCTURES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 17 April 2014, e8
-
- Article
-
- You have access
- Open access
- Export citation
Finiteness properties of cubulated groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 3 / March 2014
- Published online by Cambridge University Press:
- 10 March 2014, pp. 453-506
- Print publication:
- March 2014
-
- Article
- Export citation