Refine listing
Actions for selected content:
545 results in 20Fxx
AUTOMORPHISM GROUPS OF FREE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 341-345
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
REGULAR HYPERMAPS OVER PROJECTIVE LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 155-175
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
GROUPS AND SEMIGROUPS WITH A ONE-COUNTER WORD PROBLEM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 197-209
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
THE DENSITY OF SUBGROUP INDICES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 257-267
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
EMBEDDINGS OF COMPLEX LINE SYSTEMS AND FINITE REFLECTION GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 211-228
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Quasiregular self-mappings of manifolds and word hyperbolic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1613-1622
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
Recognizing powers in nilpotent groups and nilpotent images of free groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 83 / Issue 2 / October 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-156
- Print publication:
- October 2007
-
- Article
-
- You have access
- Export citation
On parabolic submonoids of a class of singular Artin monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 1 / February 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 29-37
- Print publication:
- February 2007
-
- Article
-
- You have access
- Export citation
The palindromic width of a free product of groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 199-208
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Cohomological characterization of the Hilbert symbol over Q*p
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 3 / December 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 361-368
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Conjugacy in singular Artin monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 183-212
- Print publication:
- October 2005
-
- Article
-
- You have access
- Export citation
Special involutions and bulky parabolic subgroups in finite Coxeter groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 1 / August 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 141-147
- Print publication:
- August 2005
-
- Article
-
- You have access
- Export citation
Fixed Point Free Actions of Groups of Exponent 5
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 3 / December 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 297-304
- Print publication:
- December 2004
-
- Article
-
- You have access
- Export citation
On groups with all subgroups almost subnormal
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 165-174
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
On Local Embedding Properties of Injectors of Finite Soluble Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 1 / February 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 23-38
- Print publication:
- February 2004
-
- Article
-
- You have access
- Export citation
An Embedding Construction for Ordered Groups: To Professor Alexander Yurievich Ol'shanskii, my teacher
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 379-392
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Group Laws Implying Virtual Nilpotence
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 74 / Issue 3 / June 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 295-312
- Print publication:
- June 2003
-
- Article
-
- You have access
- Export citation
Bounds for nilpotent-by-finite groups in certain varieties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 73 / Issue 3 / December 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 393-404
- Print publication:
- December 2002
-
- Article
-
- You have access
- Export citation
On the Toeplitz algebras of right-angled and finite-type Artin groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 2 / April 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-246
- Print publication:
- April 2002
-
- Article
-
- You have access
- Export citation
Nilpotent injectors and conjugacy classes in solvable groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-352
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
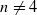 ), then every quasiregular mapping
), then every quasiregular mapping 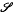 of groups including all residually or locally soluble-or-finite groups. In fact the groups of
of groups including all residually or locally soluble-or-finite groups. In fact the groups of 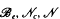 and
and 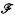 denote respectively the variety of groups of exponent dividing
denote respectively the variety of groups of exponent dividing 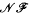 . We show that
. We show that 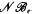 but we characterize the varieties in which that is possible. In this case, there exists a function
but we characterize the varieties in which that is possible. In this case, there exists a function 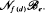 So, when
So, when 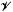 forms a variety if and only if
forms a variety if and only if 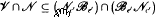 for some integers
for some integers 