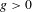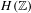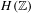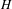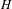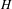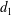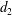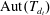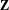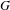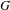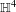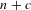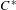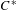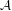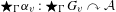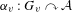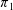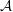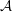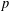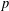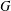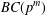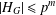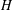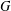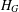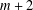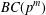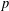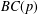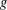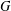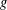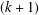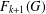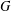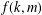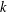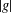Refine listing
Actions for selected content:
544 results in 20Fxx
On commensurability of right-angled Artin groups II: RAAGs defined by paths
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 559-608
- Print publication:
- May 2021
-
- Article
- Export citation
Counting subgraphs in fftp graphs with symmetry
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 2 / March 2021
- Published online by Cambridge University Press:
- 27 November 2019, pp. 327-353
- Print publication:
- March 2021
-
- Article
- Export citation
Arithmeticity of the monodromy of some Kodaira fibrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 114-157
- Print publication:
- January 2020
-
- Article
- Export citation
Cube complexes and abelian subgroups of automorphism groups of RAAGs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 20 November 2019, pp. 523-547
- Print publication:
- May 2021
-
- Article
- Export citation
ALGEBRAIC ISOMONODROMIC DEFORMATIONS AND THE MAPPING CLASS GROUP
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 18 November 2019, pp. 1497-1545
- Print publication:
- September 2021
-
- Article
- Export citation
Rigidity Properties for Hyperbolic Generalizations
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 November 2019, pp. 66-76
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Maximal hyperbolic towers and weight in the theory of free groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 18 November 2019, pp. 479-498
- Print publication:
- May 2021
-
- Article
- Export citation
Non-triviality of the Poisson boundary of random walks on the group
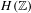 $H(\mathbb{Z})$ of Monod
$H(\mathbb{Z})$ of Monod
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 04 November 2019, pp. 1160-1189
- Print publication:
- April 2021
-
- Article
- Export citation
GROUPS WHOSE NONNORMAL SUBGROUPS ARE METAHAMILTONIAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 October 2019, pp. 96-103
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Uniformly perfect finitely generated simple left orderable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 08 October 2019, pp. 534-552
- Print publication:
- February 2021
-
- Article
- Export citation
New Simple Lattices in Products of Trees and their Projections
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 07 October 2019, pp. 1624-1690
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
A Tits alternative for topological full groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 27 August 2019, pp. 622-640
- Print publication:
- February 2021
-
- Article
- Export citation
VIRTUALLY FIBERING RIGHT-ANGLED COXETER GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 23 August 2019, pp. 957-987
- Print publication:
- May 2021
-
- Article
- Export citation
Quasi-Sturmian colorings on regular trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 09 August 2019, pp. 3403-3419
- Print publication:
- December 2020
-
- Article
- Export citation
CONJUGATING AUTOMORPHISMS OF GRAPH PRODUCTS: KAZHDAN’S PROPERTY (T) AND SQ-UNIVERSALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 07 August 2019, pp. 272-282
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
On graph products of multipliers and the Haagerup property for
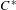 $C^{\ast }$-dynamical systems
$C^{\ast }$-dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 07 August 2019, pp. 3188-3216
- Print publication:
- December 2020
-
- Article
- Export citation
Bounded Depth Ascending HNN Extensions and
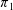 $\unicode[STIX]{x1D70B}_{1}$-Semistability at infinity
$\unicode[STIX]{x1D70B}_{1}$-Semistability at infinity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 22 July 2019, pp. 1529-1550
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
FINITE
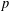 $p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
$p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 255-265
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
RIGHT ENGEL-TYPE SUBGROUPS AND LENGTH PARAMETERS OF FINITE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 340-350
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
The BNSR-invariants of the Houghton groups, concluded
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 15 July 2019, pp. 1-11
-
- Article
- Export citation