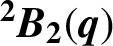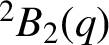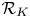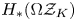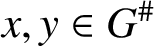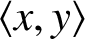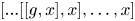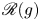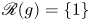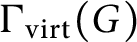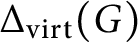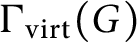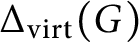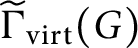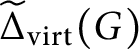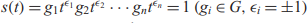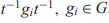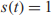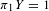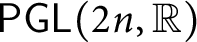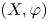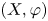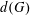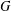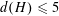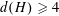Refine listing
Actions for selected content:
544 results in 20Fxx
COPRIME COMMUTATORS IN THE SUZUKI GROUPS
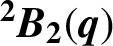 $^{\textbf{2}}{\boldsymbol{B}}_{\textbf{2}}\boldsymbol{(q)}$
$^{\textbf{2}}{\boldsymbol{B}}_{\textbf{2}}\boldsymbol{(q)}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 20 January 2021, pp. 448-452
- Print publication:
- December 2021
-
- Article
- Export citation
One-relator groups and algebras related to polyhedral products
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 15 January 2021, pp. 128-147
- Print publication:
- February 2022
-
- Article
- Export citation
THE CYCLIC GRAPH OF A Z-GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 December 2020, pp. 295-301
- Print publication:
- October 2021
-
- Article
- Export citation
ACYLINDRICAL HYPERBOLICITY OF ARTIN–TITS GROUPS ASSOCIATED WITH TRIANGLE-FREE GRAPHS AND CONES OVER SQUARE-FREE BIPARTITE GRAPHS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 01 December 2020, pp. 51-64
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Generic Newton points and the Newton poset in Iwahori-double cosets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e50
-
- Article
-
- You have access
- Open access
- Export citation
Compact groups in which all elements have countable right Engel sinks
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 13 November 2020, pp. 1790-1814
- Print publication:
- December 2021
-
- Article
- Export citation
Topological flows for hyperbolic groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3474-3520
- Print publication:
- November 2021
-
- Article
- Export citation
COMPUTABILITY, ORDERS, AND SOLVABLE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 22 October 2020, pp. 1588-1598
- Print publication:
- December 2020
-
- Article
- Export citation
The virtually generating graph of a profinite group
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 15 October 2020, pp. 808-819
- Print publication:
- December 2021
-
- Article
- Export citation
ON SOLVABILITY OF CERTAIN EQUATIONS OF ARBITRARY LENGTH OVER TORSION-FREE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 October 2020, pp. 651-659
- Print publication:
- September 2021
-
- Article
- Export citation
COHERENCE, LOCAL INDICABILITY AND NONPOSITIVE IMMERSIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 17 September 2020, pp. 659-674
- Print publication:
- March 2022
-
- Article
- Export citation
DIMENSIONAL GROUPS AND FIELDS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 918-936
- Print publication:
- September 2020
-
- Article
- Export citation
On semidirectly closed non-aperiodic pseudovarieties of finite monoids
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 24 August 2020, pp. 913-928
-
- Article
- Export citation
Rigidity of diagonally embedded triangle groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 20 August 2020, pp. 560-579
- Print publication:
- September 2021
-
- Article
- Export citation
The Klein bottle group is not strongly verbally closed, though awfully close to being so
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 03 August 2020, pp. 491-497
- Print publication:
- June 2021
-
- Article
- Export citation
Groups of piecewise linear homeomorphisms of flows
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1595-1622
- Print publication:
- August 2020
-
- Article
- Export citation
GENERATING MAXIMAL SUBGROUPS OF FINITE ALMOST SIMPLE GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e32
-
- Article
-
- You have access
- Open access
- Export citation
Positive definite functions and cut-off for discrete groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 22 June 2020, pp. 306-322
- Print publication:
- June 2021
-
- Article
- Export citation
Relative vertex asphericity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 June 2020, pp. 292-305
- Print publication:
- June 2021
-
- Article
- Export citation
Big mapping class groups and rigidity of the simple circle
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 03 June 2020, pp. 1961-1987
- Print publication:
- July 2021
-
- Article
- Export citation