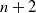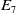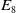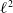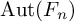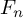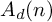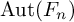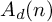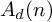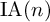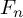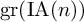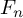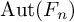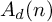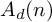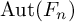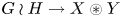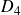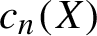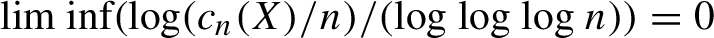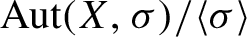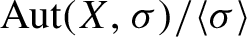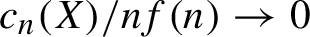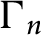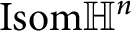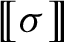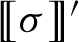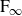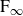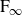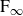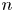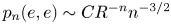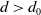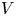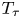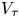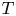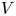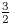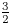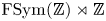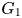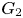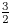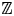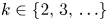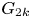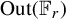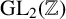Refine listing
Actions for selected content:
543 results in 20Fxx
Enriques surfaces and an Apollonian packing in eight dimensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 205-221
- Print publication:
- January 2023
-
- Article
- Export citation
A note on the rational homological dimension of lattices in positive characteristic
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 10 June 2022, pp. 138-140
- Print publication:
- January 2023
-
- Article
- Export citation
ACTIONS OF AUTOMORPHISM GROUPS OF FREE GROUPS ON SPACES OF JACOBI DIAGRAMS. II
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 June 2022, pp. 1-69
- Print publication:
- January 2024
-
- Article
- Export citation
Lamplighter groups, median spaces and Hilbertian geometry
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 09 June 2022, pp. 500-529
-
- Article
- Export citation
Bouquets of curves in surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 90-97
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isometric actions and finite approximations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 2464-2470
- Print publication:
- July 2023
-
- Article
- Export citation
Groups generated by two twists along spherical sequences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 16 May 2022, pp. 137-161
- Print publication:
- January 2023
-
- Article
- Export citation
Left regular representations of Garside categories I. C*-algebras and groupoids
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. S53-S86
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Local finiteness and automorphism groups of low complexity subshifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 18 April 2022, pp. 1980-2001
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Special cube complexes revisited: a quasi-median generalization
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 11 April 2022, pp. 743-777
- Print publication:
- June 2023
-
- Article
- Export citation
Hyperbolic Coxeter groups of minimal growth rates in higher dimensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 06 April 2022, pp. 232-242
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topological full groups of minimal subshifts and quantifying local embeddings into finite groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 1492-1510
- Print publication:
- May 2023
-
- Article
- Export citation
The BNSR-invariants of the Lodha–Moore groups, and an exotic simple group of type
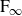 $\textrm{F}_\infty$
$\textrm{F}_\infty$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 04 April 2022, pp. 25-48
- Print publication:
- January 2023
-
- Article
- Export citation
Local limit theorems in relatively hyperbolic groups II: the non-spectrally degenerate case
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 764-830
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Property (T) in k-gonal random groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 22 February 2022, pp. 734-738
- Print publication:
- September 2022
-
- Article
- Export citation
Irrational-slope versions of thompson's groups T and V
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 February 2022, pp. 244-262
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuity of critical exponent of quasiconvex-cocompact groups under Gromov–Hausdorff convergence
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 10 February 2022, pp. 1189-1221
- Print publication:
- April 2023
-
- Article
- Export citation
On the spread of infinite groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 214-228
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thermodynamic metrics on outer space
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 03 February 2022, pp. 729-793
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AUTOMORPHISM AND OUTER AUTOMORPHISM GROUPS OF RIGHT-ANGLED ARTIN GROUPS ARE NOT RELATIVELY HYPERBOLIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 102-112
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation