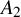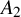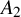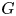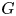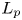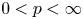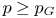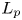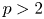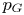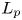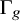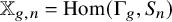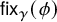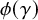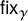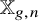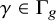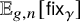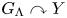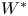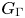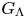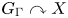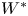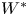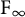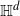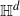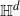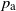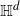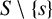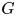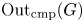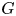Refine listing
Actions for selected content:
542 results in 20Fxx
A note on virtual duality and automorphism groups of right-angled Artin groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 573-581
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Baumslag–Solitar groups and residual nilpotence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 532-547
-
- Article
- Export citation
q-deformed rational numbers and the 2-Calabi–Yau category of type
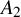 $A_{2}$
$A_{2}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 June 2023, e47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isometric actions on Lp-spaces: dependence on the value of p
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1300-1313
- Print publication:
- June 2023
-
- Article
- Export citation
The Asymptotic Statistics of Random Covering Surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 May 2023, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Jordan–Hölder theorem for skew left braces and their applications to multipermutation solutions of the Yang–Baxter equation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 793-809
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relatively hyperbolic groups with strongly shortcut parabolics are strongly shortcut
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 17 April 2023, pp. 367-380
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orbit equivalence rigidity of irreducible actions of right-angled Artin groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 860-887
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite image homomorphisms of the braid group and its generalizations
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 23 March 2023, pp. 430-445
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MULTIPLICATION TABLES AND WORD-HYPERBOLICITY IN FREE PRODUCTS OF SEMIGROUPS, MONOIDS AND GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 17 March 2023, pp. 396-430
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Braiding groups of automorphisms and almost-automorphisms of trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 March 2023, pp. 555-593
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thin-ended clusters in percolation in
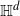 $\mathbb{H}^d$
$\mathbb{H}^d$
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 10 March 2023, pp. 581-610
- Print publication:
- June 2023
-
- Article
- Export citation
Isolations of geodesic planes in the frame bundle of a hyperbolic 3-manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 488-529
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FINITE GROUPS WITH INDEPENDENT GENERATING SETS OF ONLY TWO SIZES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 23 February 2023, pp. 449-458
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Subsymmetric exchanged braids and the Burau matrix
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 10 February 2023, pp. 154-187
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On automorphisms and splittings of special groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 10 February 2023, pp. 232-305
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conjugacy growth in the higher Heisenberg groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 23 January 2023, pp. S148-S169
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolically embedded subgroups and quasi-isometries of pairs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 10 January 2023, pp. 827-843
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative hyperbolicity of free-by-cyclic extensions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 30 January 2023, pp. 153-183
- Print publication:
- January 2023
-
- Article
- Export citation
STRUCTURAL STABILITY OF MEANDERING-HYPERBOLIC GROUP ACTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 753-810
- Print publication:
- March 2024
-
- Article
- Export citation