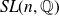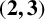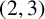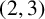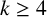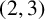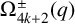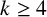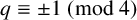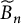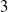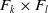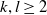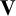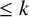Refine listing
Actions for selected content:
545 results in 20Fxx
Affine Bruhat order and Demazure products
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 15 April 2024, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zariski dense surface subgroups in
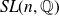 $SL(n,\mathbb{Q})$ with odd
$SL(n,\mathbb{Q})$ with odd  $n$
$n$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 26 March 2024, pp. 643-653
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite skew braces of square-free order and supersolubility
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 March 2024, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Examples of hyperbolic spaces without the properties of quasi-ball or bounded eccentricity
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 11 March 2024, pp. 440-448
- Print publication:
- May 2024
-
- Article
- Export citation
Hyperfiniteness of boundary actions of acylindrically hyperbolic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 March 2024, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Patterson–Sullivan theory for groups with a strongly contracting element
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 3216-3271
- Print publication:
- November 2024
-
- Article
- Export citation
THE
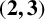 $\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
$\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 130-148
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum: A certain structure of Artin groups and the isomorphism conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 23 February 2024, pp. 729-730
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation
PERFECTING GROUP SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 2549-2591
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LIMIT SETS OF UNFOLDING PATHS IN OUTER SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 15 February 2024, pp. 2365-2403
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shi arrangements and low elements in affine Coxeter groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 12 February 2024, pp. 683-713
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPLETE EMBEDDINGS OF GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 26 January 2024, pp. 136-144
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A HOMOMORPHISM BETWEEN BOTT–SAMELSON BIMODULES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 256 / December 2024
- Published online by Cambridge University Press:
- 22 January 2024, pp. 761-784
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dehn functions of mapping tori of right-angled Artin groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 252-289
- Print publication:
- May 2024
-
- Article
- Export citation
Classifying spaces for families of abelian subgroups of braid groups, RAAGs and graphs of abelian groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 290-307
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE PRO-
 $\boldsymbol {k}$-SOLVABLE TOPOLOGY ON A FREE GROUP
$\boldsymbol {k}$-SOLVABLE TOPOLOGY ON A FREE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 363-383
- Print publication:
- June 2024
-
- Article
- Export citation
The spherical growth series of Dyer groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 December 2023, pp. 168-187
-
- Article
- Export citation
Levy and Thurston obstructions of finite subdivision rules
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 2649-2699
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON RESIDUES AND CONJUGACIES FOR GERMS OF 1-D PARABOLIC DIFFEOMORPHISMS IN FINITE REGULARITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 01 December 2023, pp. 1821-1855
- Print publication:
- July 2024
-
- Article
- Export citation
ON GROUPS OF UNITS OF SPECIAL AND ONE-RELATOR INVERSE MONOIDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 21 November 2023, pp. 1875-1918
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation