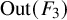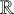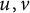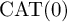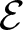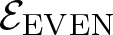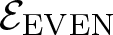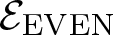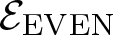Refine listing
Actions for selected content:
545 results in 20Fxx
Are free groups of different ranks bi-invariantly quasi-isometric?
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 356-364
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The conjugacy problem for
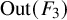 $\operatorname {Out}(F_3)$
$\operatorname {Out}(F_3)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 February 2025, e41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolic Metric Spaces and Stochastic Embeddings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Right-angled Artin groups and the cohomology basis graph
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 634-654
-
- Article
- Export citation
Bender–Knuth Billiards in Coxeter Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Membership problems for positive one-relator groups and one-relation monoids
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 January 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Automorphisms of fine curve graphs for nonorientable surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 16 January 2025, pp. 232-244
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
OMEGA-CATEGORICAL PSEUDOFINITE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 January 2025, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A characterization of virtually free groups among hyperbolic groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 477-483
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized torsion orders and Alexander polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 401-420
- Print publication:
- June 2025
-
- Article
- Export citation
PROPER
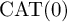 $\mathrm {CAT(0)}$ ACTIONS OF UNIPOTENT-FREE LINEAR GROUPS
$\mathrm {CAT(0)}$ ACTIONS OF UNIPOTENT-FREE LINEAR GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 587-601
- Print publication:
- March 2025
-
- Article
- Export citation
THE DECOMPOSITION OF PERMUTATION MODULE FOR INFINITE CHEVALLEY GROUPS, II
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 27 December 2024, pp. 156-169
- Print publication:
- March 2025
-
- Article
- Export citation
Order-automorphism groups of Archimedean ordered groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 628-633
- Print publication:
- June 2025
-
- Article
- Export citation
Ideals of equations for elements in a free group and Stallings folding
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 19 December 2024, pp. 421-462
-
- Article
- Export citation
A note on the splittings of finitely presented Bestvina–Brady groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 19 December 2024, pp. 224-227
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite presentability of twisted Brin–Thompson groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 December 2024, pp. 1-22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on right-nil and strong-nil skew braces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 December 2024, pp. 1-9
-
- Article
- Export citation
Limit trees for free group automorphisms: universality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e122
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The planar 3-colorable subgroup ε of Thompson’s group F and its even part
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 173-197
-
- Article
- Export citation
Random walks on groups and superlinear-divergent geodesics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 21 November 2024, pp. 1403-1443
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation