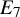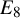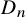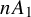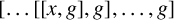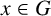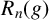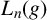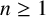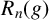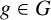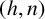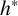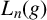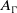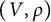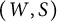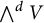Refine listing
Actions for selected content:
545 results in 20Fxx
Orthogonal roots, Macdonald representations, and quasiparabolic sets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 July 2025, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Thompson’s group T has quadratic Dehn function
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 July 2025, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH DENSE TRANSITIVELY NORMAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-7
-
- Article
- Export citation
The Hanna Neumann conjecture for graphs of free groups with cyclic edge groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1576-1614
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Random walks and contracting elements I: deviation inequality and limit laws
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 1512-1575
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIGHT ENGEL CONDITIONS FOR ORDERABLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 June 2025, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rotation groups virtually embed into right-angled rotation groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1-25
-
- Article
- Export citation
On Thompson groups for Ważewski dendrites
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 189-231
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Formanek-Procesi group with base a right-angled Artin group: Lie algebra and residual nilpotence
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 13 May 2025, pp. 1-22
-
- Article
- Export citation
The nonabelian product modulo sum
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1069-1109
-
- Article
- Export citation
On Growth Functions of Coxeter Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 979-993
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rigidity of mapping class groups MOD powers of twists
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 07 April 2025, pp. 1-71
-
- Article
- Export citation
3-manifold spine cyclic presentations with seldom seen Whitehead graphs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 04 April 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A hyperbolic free-by-cyclic group determined by its finite quotients
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 500-502
- Print publication:
- September 2025
-
- Article
- Export citation
The Klein bottle has stably unbounded homeomorphism group
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 04 April 2025, pp. 494-499
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tree-like graphings, wallings, and median graphings of equivalence relations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 March 2025, e64
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On exterior powers of reflection representations, II
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-23
-
- Article
- Export citation
A Shelah group in ZFC
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Pride–Guba–Sapir exact sequence for the relation bimodule of an associative algebra
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 467-474
- Print publication:
- September 2025
-
- Article
- Export citation
Stratified braid groups: monodromy
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 259-292
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation