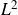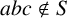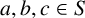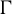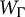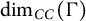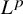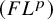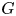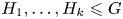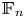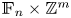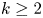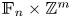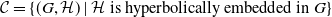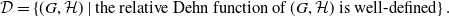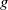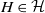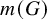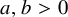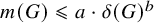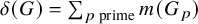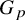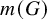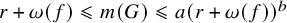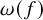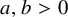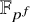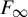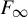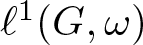Refine listing
Actions for selected content:
542 results in 20Fxx
Distortion element in the automorphism group of a full shift
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 1757-1817
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TORIC REFLECTION GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 18 October 2023, pp. 171-199
- Print publication:
- April 2024
-
- Article
- Export citation
On subdirect products of type FPn of limit groups over Droms RAAGs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 11 October 2023, pp. 417-440
- Print publication:
- March 2024
-
- Article
- Export citation
ON EXTERIOR POWERS OF REFLECTION REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 90-102
- Print publication:
- August 2024
-
- Article
- Export citation
TRIPLE-PRODUCT-FREE SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 06 October 2023, pp. 129-135
- Print publication:
- August 2024
-
- Article
- Export citation
A new upper bound for the asymptotic dimension of RACGs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 04 October 2023, pp. 338-349
- Print publication:
- June 2024
-
- Article
- Export citation
Some torsion-free solvable groups with few subquotients
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 279-286
- Print publication:
- March 2024
-
- Article
- Export citation
Stability for hyperbolic groups acting on boundary spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 21 September 2023, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Żuk’s criterion for Banach spaces and random groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 September 2023, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intersection configurations in free and free times free-abelian groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 11 September 2023, pp. 1552-1582
- Print publication:
- October 2024
-
- Article
- Export citation
Fixed point conditions for non-coprime actions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 345-351
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cusps, Kleinian groups, and Eisenstein series
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 31 August 2023, e75
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative Dehn functions, hyperbolically embedded subgroups and combination theorems
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 25 August 2023, pp. 1-23
- Print publication:
- January 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The maximal size of a minimal generating set
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 August 2023, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A presentation for the Eisenstein-Picard modular group in three complex dimensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 25 July 2023, pp. 625-654
- Print publication:
- September 2023
-
- Article
- Export citation
HALL CLASSES OF GROUPS WITH A LOCALLY FINITE OBSTRUCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 16-43
- Print publication:
- August 2024
-
- Article
- Export citation
Finitely presented left orderable monsters
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 06 July 2023, pp. 1367-1378
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Dales–Żelazko conjecture for Beurling algebras on discrete groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 03 July 2023, pp. 613-624
-
- Article
- Export citation
Groups of small period growth
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 27 June 2023, pp. 625-641
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuously many quasi-isometry classes of residually finite groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 569-572
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation