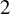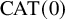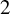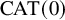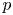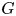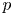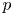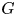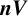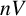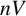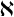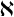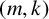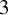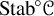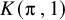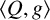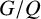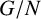Refine listing
Actions for selected content:
543 results in 20Fxx
STRUCTURAL STABILITY OF MEANDERING-HYPERBOLIC GROUP ACTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 753-810
- Print publication:
- March 2024
-
- Article
- Export citation
Tits Alternative for
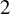 $2$-dimensional
$2$-dimensional 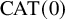 $\mathrm {CAT}(0)$ complexes
$\mathrm {CAT}(0)$ complexes
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 December 2022, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rational growth in torus bundle groups of odd trace
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 06 December 2022, pp. 1080-1132
-
- Article
- Export citation
Conjugacy conditions for supersoluble complements of an abelian base and a fixed point result for non-coprime actions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 24 November 2022, pp. 1075-1079
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Decidability problem for exponential equations in finitely presented groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 22 November 2022, pp. 731-748
- Print publication:
- September 2023
-
- Article
- Export citation
The fundamental inequality for cocompact Fuchsian groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 November 2022, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Curves on the torus intersecting at most k times
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 15 November 2022, pp. 569-584
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PERMUTATION-BASED PRESENTATIONS FOR BRIN’S HIGHER-DIMENSIONAL THOMPSON GROUPS
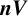 $\boldsymbol {nV}$
$\boldsymbol {nV}$
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 116 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 15 November 2022, pp. 39-67
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Yet another Freiheitssatz: Mating finite groups with locally indicable ones
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 14 November 2022, pp. 337-344
- Print publication:
- May 2023
-
- Article
- Export citation
Intersection of parabolic subgroups in even Artin groups of FC-type
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 18 October 2022, pp. 938-957
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Central limit theorems for counting measures in coarse negative curvature
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 03 November 2022, pp. 1980-2013
- Print publication:
- October 2022
-
- Article
- Export citation
GROUPS IN WHICH ALL LARGE SUBGROUPS HAVE BOUNDED NEAR DEFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 456-463
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Products of derangements in simple permutation groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 23 September 2022, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parabolic subgroups of large-type Artin groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 September 2022, pp. 393-414
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small non-Leighton two-complexes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 385-391
- Print publication:
- March 2023
-
- Article
- Export citation
Stability conditions for contraction algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 02 September 2022, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Hanna Neumann conjecture for surface groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 12 October 2022, pp. 1850-1877
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SYLOW CLASSES OF REFLECTION SUBGROUPS AND PSEUDO-LEVI SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 30 August 2022, pp. 508-510
- Print publication:
- December 2022
-
- Article
-
- You have access
- HTML
- Export citation
Maximal order Abelian subgroups of Coxeter groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 02 August 2022, pp. 114-120
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GROUPS WITH A LARGE PERMUTABLY EMBEDDED SUBGROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 276-283
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation