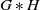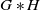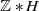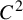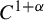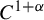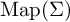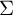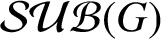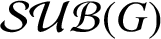Refine listing
Actions for selected content:
543 results in 20Fxx
Weak amenability of free products of hyperbolic and amenable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 698-701
- Print publication:
- September 2022
-
- Article
- Export citation
Commutator length of powers in free products of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 102-119
-
- Article
- Export citation
Invariants for metabelian groups of prime power exponent, colorings, and stairs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 December 2021, pp. 267-297
- Print publication:
- February 2023
-
- Article
- Export citation
Polynomiality of factorizations in reflection groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 09 December 2021, pp. 245-266
- Print publication:
- February 2023
-
- Article
- Export citation
Some embeddings between symmetric R. thompson groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 07 December 2021, pp. 1-18
-
- Article
- Export citation
Abelian actions on compact nonorientable Riemann surfaces
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 December 2021, pp. 634-648
- Print publication:
- September 2022
-
- Article
- Export citation
Folding-like techniques for CAT(0) cube complexes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 28 October 2021, pp. 227-238
- Print publication:
- July 2022
-
- Article
- Export citation
The type semigroup, comparison, and almost finiteness for ample groupoids
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 27 October 2021, pp. 361-400
- Print publication:
- February 2023
-
- Article
- Export citation
A bimodule description of the Hecke category
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 30 September 2021, pp. 2133-2159
- Print publication:
- October 2021
-
- Article
- Export citation
On holomorphic reflexivity conditions for complex Lie groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 30 September 2021, pp. 800-821
-
- Article
- Export citation
Strongly aperiodic subshifts of finite type on hyperbolic groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 09 September 2021, pp. 2740-2783
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Examples of distorted interval diffeomorphisms of intermediate regularity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 08 September 2021, pp. 3311-3324
- Print publication:
- November 2022
-
- Article
- Export citation
Right-angled Artin groups as normal subgroups of mapping class groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 27 July 2021, pp. 1807-1852
- Print publication:
- August 2021
-
- Article
- Export citation
Symmetry of Narayana Numbers and Rowvacuation of Root Posets
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 July 2021, e53
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NORMAL REFLECTION SUBGROUPS OF COMPLEX REFLECTION GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 21 July 2021, pp. 879-917
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON GROUPS WHOSE SUBGROUPS ARE EITHER MODULAR OR CONTRANORMAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 18 June 2021, pp. 286-295
- Print publication:
- April 2022
-
- Article
- Export citation
SYMÉTRIES ET TRANSVEXIONS, PRINCIPALEMENT DANS LES GROUPES DE RANG DE MORLEY FINI SANS INVOLUTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 June 2021, pp. 965-990
- Print publication:
- September 2021
-
- Article
- Export citation
COMMUTATOR EQUATIONS IN FINITE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 320-335
- Print publication:
- May 2022
-
- Article
- Export citation
BIG MAPPING CLASS GROUPS WITH HYPERBOLIC ACTIONS: CLASSIFICATION AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 31 May 2021, pp. 2173-2204
- Print publication:
- November 2022
-
- Article
- Export citation
ON THE CONNECTEDNESS OF THE CHABAUTY SPACE OF A LOCALLY COMPACT PRONILPOTENT GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 161-170
- Print publication:
- February 2022
-
- Article
- Export citation