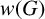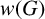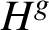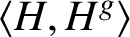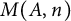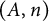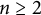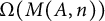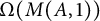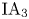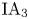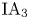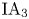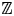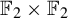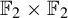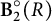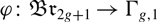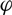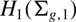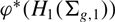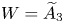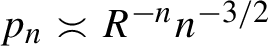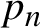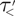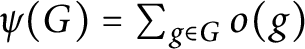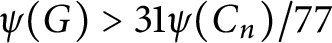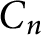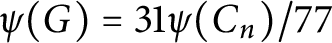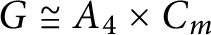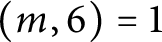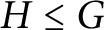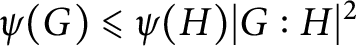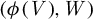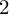Refine listing
Actions for selected content:
544 results in 20Fxx
ON THE CONNECTEDNESS OF THE CHABAUTY SPACE OF A LOCALLY COMPACT PRONILPOTENT GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 161-170
- Print publication:
- February 2022
-
- Article
- Export citation
ON THE RANK OF A VERBAL SUBGROUP OF A FINITE GROUP
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 12 May 2021, pp. 145-159
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- Export citation
GROUPS WITH MANY PRONORMAL SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 75-86
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
On homotopy nilpotency of loop spaces of Moore spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 296-307
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the low-dimensional cohomology groups of the IA-automorphism group of the free group of rank three
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 05 May 2021, pp. 338-363
-
- Article
-
- You have access
- Open access
- Export citation
Dynamic asymptotic dimension for actions of virtually cyclic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 May 2021, pp. 364-372
-
- Article
- Export citation
On sofic approximations of
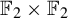 ${\mathbb F}_2\times {\mathbb F}_2$
${\mathbb F}_2\times {\mathbb F}_2$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 2333-2351
- Print publication:
- July 2022
-
- Article
- Export citation
Infinitely presented permutation stable groups and invariant random subgroups of metabelian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 30 April 2021, pp. 2028-2063
- Print publication:
- June 2022
-
- Article
- Export citation
On the Finiteness length of some soluble linear groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 21 April 2021, pp. 1209-1243
- Print publication:
- October 2022
-
- Article
- Export citation
BEING CAYLEY AUTOMATIC IS CLOSED UNDER TAKING WREATH PRODUCT WITH VIRTUALLY CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 13 April 2021, pp. 464-474
- Print publication:
- December 2021
-
- Article
- Export citation
Lower central series, surface braid groups, surjections and permutations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 05 April 2021, pp. 373-399
- Print publication:
- March 2022
-
- Article
- Export citation
Braid groups, mapping class groups and their homology with twisted coefficients
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 05 April 2021, pp. 249-266
- Print publication:
- March 2022
-
- Article
- Export citation
2-dimensional Coxeter groups are biautomatic
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 23 March 2021, pp. 382-401
- Print publication:
- April 2022
-
- Article
- Export citation
Local limit theorems in relatively hyperbolic groups I: rough estimates
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 23 March 2021, pp. 1926-1966
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- Export citation
Higher horospherical limit sets for G-modules over CAT(0)-spaces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 12 March 2021, pp. 133-163
- Print publication:
- July 2021
-
- Article
- Export citation
Generalized small cancellation conditions, non-positive curvature and diagrammatic reducibility
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 02 March 2021, pp. 545-566
- Print publication:
- June 2022
-
- Article
- Export citation
Divergence and quasi-isometry classes of random Gromov’s monsters
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 18 February 2021, pp. 249-264
- Print publication:
- September 2021
-
- Article
- Export citation
On two conjectures about the sum of element orders
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 26 January 2021, pp. 30-38
- Print publication:
- March 2022
-
- Article
- Export citation
BOUNDNESS OF INTERSECTION NUMBERS FOR ACTIONS BY TWO-DIMENSIONAL BIHOLOMORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 1677-1700
- Print publication:
- September 2022
-
- Article
- Export citation
ON THE PRONORM OF A GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 20 January 2021, pp. 287-294
- Print publication:
- October 2021
-
- Article
- Export citation