Refine listing
Actions for selected content:
46 results in 20Kxx
Regulating hulls of almost completely decomposable groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-155
- Print publication:
- April 1993
-
- Article
-
- You have access
- Export citation
Type radicals and quasi-decompositions of torsion-free abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 2 / April 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 219-236
- Print publication:
- April 1992
-
- Article
-
- You have access
- Export citation
Annihilator equivalence of torsion-free abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 1 / February 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 119-129
- Print publication:
- February 1992
-
- Article
-
- You have access
- Export citation
Abelian groups with small cotorsion images
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 243-247
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
Constructions of Σ-groups, relatively free Σ-groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 1 / February 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 8-21
- Print publication:
- February 1989
-
- Article
-
- You have access
- Export citation
Endomorphism rings of Butler groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 3 / June 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 322-329
- Print publication:
- June 1987
-
- Article
-
- You have access
- Export citation
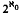 is cotorsion, is
is cotorsion, is 