Refine listing
Actions for selected content:
44 results in 20Kxx
On n-Sums in an Abelian Group
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 419-435
-
- Article
- Export citation
ON A PARTITION PROBLEM OF FINITE ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 29 April 2015, pp. 24-31
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
STRONGLY INVARIANT SUBGROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 431-443
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
THE CLASS OF (2, 2)-GROUPS WITH HOMOCYCLIC REGULATOR QUOTIENT OF EXPONENT
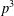 $p^{3}$ HAS BOUNDED REPRESENTATION TYPE
$p^{3}$ HAS BOUNDED REPRESENTATION TYPE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 04 December 2014, pp. 12-29
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
ON SI-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 12 September 2014, pp. 92-103
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
COMMUTING PROPERTIES OF EXT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 25 February 2013, pp. 276-288
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
On the abelianization of derived categories and a negative solution to Rosický’s problem
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 06 November 2012, pp. 125-147
- Print publication:
- January 2013
-
- Article
- Export citation
DIAGRAMS OF AN ABELIAN GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 1 / August 2009
- Published online by Cambridge University Press:
- 06 July 2009, pp. 38-64
- Print publication:
- August 2009
-
- Article
-
- You have access
- Export citation
SELF-SMALL ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 29 June 2009, pp. 205-216
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
VARIETIES OF ABELIAN TOPOLOGICAL GROUPS AND SCATTERED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 487-495
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Monothetic algebraic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 315-324
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Valuated Butler groups of finite rank
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 335-350
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Abelian groups whose subgroup lattice is the union of two intervals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 78 / Issue 1 / February 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 27-36
- Print publication:
- February 2005
-
- Article
-
- You have access
- Export citation
Endoprimal abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 3 / December 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 412-428
- Print publication:
- December 1999
-
- Article
-
- You have access
- Export citation
Lattice embeddings of abelian prime power groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 2 / April 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 259-278
- Print publication:
- April 1997
-
- Article
-
- You have access
- Export citation
Regulating hulls of almost completely decomposable groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 2 / April 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 143-155
- Print publication:
- April 1993
-
- Article
-
- You have access
- Export citation
Type radicals and quasi-decompositions of torsion-free abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 2 / April 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 219-236
- Print publication:
- April 1992
-
- Article
-
- You have access
- Export citation
Annihilator equivalence of torsion-free abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 1 / February 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 119-129
- Print publication:
- February 1992
-
- Article
-
- You have access
- Export citation
Abelian groups with small cotorsion images
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 2 / April 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 243-247
- Print publication:
- April 1991
-
- Article
-
- You have access
- Export citation
Imbedded subgroups of abelian groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 2 / April 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-298
- Print publication:
- April 1990
-
- Article
-
- You have access
- Export citation
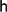
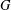
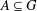
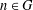
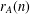
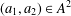
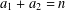
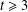

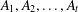
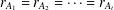
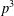

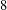
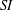
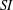
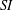
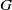
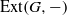
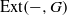
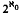 is cotorsion, is
is cotorsion, is 