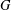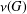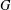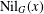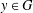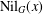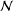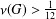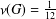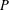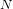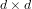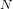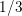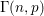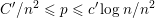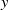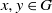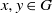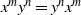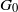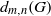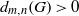Refine listing
Actions for selected content:
30 results in 20Pxx
Probability and Bias in Generating Supersoluble Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 4 / November 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 899-909
-
- Article
- Export citation
ON THE PROBABILITY OF GENERATING NILPOTENT SUBGROUPS IN A FINITE GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 20 November 2015, pp. 447-453
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
THE SUBGROUP COMMUTATIVITY DEGREE OF FINITE
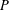 $P$-GROUPS
$P$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 37-41
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Virtual geometricity is rare
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 July 2015, pp. 444-455
-
- Article
-
- You have access
- Export citation
Nilpotent-independent sets and estimation in matrix algebras
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 May 2015, pp. 404-418
-
- Article
-
- You have access
- Export citation
Random triangular groups at density
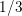 $1/3$
$1/3$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 27 November 2014, pp. 167-178
- Print publication:
- January 2015
-
- Article
- Export citation
COMMUTATIVITY DEGREE OF A CLASS OF FINITE GROUPS AND CONSEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 30 January 2013, pp. 448-452
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
THE PROBABILITY THAT
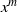 $\lowercase {X}^{\lowercase {M}}$ AND
$\lowercase {X}^{\lowercase {M}}$ AND 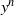 $\lowercase {Y}^{\lowercase {N}}$ COMMUTE IN A COMPACT GROUP
$\lowercase {Y}^{\lowercase {N}}$ COMMUTE IN A COMPACT GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 02 August 2012, pp. 503-513
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
ON A NONABELIAN BALOG–SZEMERÉDI-TYPE LEMMA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 08 June 2010, pp. 127-132
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
On the probability of generating a minimal d-generated group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 2 / October 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 177-186
- Print publication:
- October 2001
-
- Article
-
- You have access
- Export citation