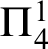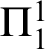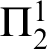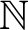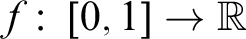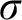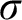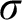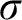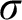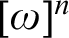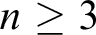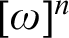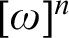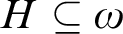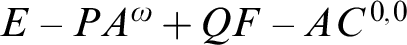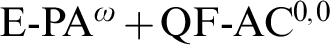Refine listing
Actions for selected content:
275 results in 03BXX
THE SEMANTIC FOUNDATIONS OF PHILOSOPHICAL ANALYSIS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 22 February 2021, pp. 603-623
- Print publication:
- June 2023
-
- Article
- Export citation
WELL ORDERING PRINCIPLES AND
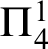 ${\Pi }^{1}_{4}$-STATEMENTS: A PILOT STUDY
${\Pi }^{1}_{4}$-STATEMENTS: A PILOT STUDY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 February 2021, pp. 709-745
- Print publication:
- June 2021
-
- Article
- Export citation
RECURSIVE AXIOMATISATIONS FROM SEPARATION PROPERTIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 03 February 2021, pp. 1228-1258
- Print publication:
- September 2021
-
- Article
- Export citation
THE REVERSE MATHEMATICS OF THEOREMS OF JORDAN AND LEBESGUE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1657-1675
- Print publication:
- December 2021
-
- Article
- Export citation
TWO-VARIABLE LOGIC HAS WEAK, BUT NOT STRONG, BETH DEFINABILITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 785-800
- Print publication:
- June 2021
-
- Article
- Export citation
CHARACTERIZING EXISTENCE OF A MEASURABLE CARDINAL VIA MODAL LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 162-177
- Print publication:
- March 2021
-
- Article
- Export citation
THE OPEN AND CLOPEN RAMSEY THEOREMS IN THE WEIHRAUCH LATTICE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 316-351
- Print publication:
- March 2021
-
- Article
- Export citation
WHAT IS A RULE OF INFERENCE?
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 21 December 2020, pp. 307-346
- Print publication:
- June 2021
-
- Article
- Export citation
BINARY KRIPKE SEMANTICS FOR A STRONG LOGIC FOR NAIVE TRUTH
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 December 2020, pp. 668-692
- Print publication:
- September 2022
-
- Article
- Export citation
THE MODAL LOGIC OF
 $\sigma $-CENTERED FORCING AND RELATED FORCING CLASSES
$\sigma $-CENTERED FORCING AND RELATED FORCING CLASSES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 03 December 2020, pp. 1-24
- Print publication:
- March 2021
-
- Article
- Export citation
COMPUTABILITY IN PARTIAL COMBINATORY ALGEBRAS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 05 January 2021, pp. 224-240
- Print publication:
- December 2020
-
- Article
-
- You have access
- Open access
- Export citation
The Brouwer invariance theorems in reverse mathematics
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e51
-
- Article
-
- You have access
- Open access
- Export citation
INQUISITIVE BISIMULATION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 77-109
- Print publication:
- March 2021
-
- Article
- Export citation
WEIHRAUCH GOES BROUWERIAN
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 1614-1653
- Print publication:
- December 2020
-
- Article
- Export citation
RAMSEY-LIKE THEOREMS AND MODULI OF COMPUTATION
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 27 October 2020, pp. 72-108
- Print publication:
- March 2022
-
- Article
- Export citation
THE MODAL LOGICS OF KRIPKE–FEFERMAN TRUTH
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 27 October 2020, pp. 362-396
- Print publication:
- March 2021
-
- Article
- Export citation
THE CHARACTERIZATION OF WEIHRAUCH REDUCIBILITY IN SYSTEMS CONTAINING
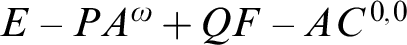 $E-PA^{\omega } + QF-AC^{0,0}$
$E-PA^{\omega } + QF-AC^{0,0}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 27 October 2020, pp. 224-261
- Print publication:
- March 2021
-
- Article
- Export citation
DOING WITHOUT ACTION TYPES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 380-410
- Print publication:
- June 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXPLORING THE LANDSCAPE OF RELATIONAL SYLLOGISTIC LOGICS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 728-765
- Print publication:
- September 2021
-
- Article
- Export citation
SEMANTICS FOR PURE THEORIES OF CONNEXIVE IMPLICATION
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 October 2020, pp. 591-606
- Print publication:
- September 2022
-
- Article
- Export citation