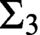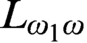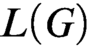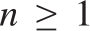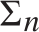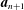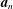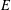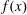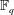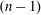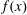Refine listing
Actions for selected content:
169 results in 03DXX
SOLVING DIFFERENCE EQUATIONS IN SEQUENCES: UNIVERSALITY AND UNDECIDABILITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 30 June 2020, e33
-
- Article
-
- You have access
- Open access
- Export citation
GÖDEL’S SECOND INCOMPLETENESS THEOREM: HOW IT IS DERIVED AND WHAT IT DELIVERS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 3-4 / December 2020
- Published online by Cambridge University Press:
- 10 June 2020, pp. 241-256
- Print publication:
- December 2020
-
- Article
- Export citation
HOW STRONG ARE SINGLE FIXED POINTS OF NORMAL FUNCTIONS?
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 709-732
- Print publication:
- June 2020
-
- Article
- Export citation
CODING IN GRAPHS AND LINEAR ORDERINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 673-690
- Print publication:
- June 2020
-
- Article
- Export citation
COMPUTABLE LINEAR ORDERS AND PRODUCTS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 605-623
- Print publication:
- June 2020
-
- Article
- Export citation
AN APPLICATION OF RECURSION THEORY TO ANALYSIS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 26 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 11 June 2020, pp. 15-25
- Print publication:
- March 2020
-
- Article
- Export citation
The expressiveness of quasiperiodic and minimal shifts of finite type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 22 January 2020, pp. 1086-1138
- Print publication:
- April 2021
-
- Article
- Export citation
A LEARNING-THEORETIC CHARACTERISATION OF MARTIN-LÖF RANDOMNESS AND SCHNORR RANDOMNESS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 04 November 2019, pp. 531-549
- Print publication:
- June 2021
-
- Article
- Export citation
EFFECTIVE INSEPARABILITY, LATTICES, AND PREORDERING RELATIONS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 14 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 12 July 2019, pp. 838-865
- Print publication:
- December 2021
-
- Article
- Export citation
DNR AND INCOMPARABLE TURING DEGREES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 06 April 2016, e7
-
- Article
-
- You have access
- Open access
- Export citation
ANALYTIC EQUIVALENCE RELATIONS SATISFYING HYPERARITHMETIC-IS-RECURSIVE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 3 / 2015
- Published online by Cambridge University Press:
- 27 April 2015, e8
-
- Article
-
- You have access
- Open access
- Export citation
Computing boundary extensions of conformal maps
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 September 2014, pp. 360-378
-
- Article
-
- You have access
- Export citation
Deterministic polynomial factoring and association schemes
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 123-140
-
- Article
-
- You have access
- Export citation
The complexity of the four colour theorem
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 13 / January 2010
- Published online by Cambridge University Press:
- 01 August 2010, pp. 414-425
-
- Article
-
- You have access
- Export citation
Une dualité entre fonctions booléennes
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 26 April 2010, pp. 633-652
- Print publication:
- July 2010
-
- Article
- Export citation
Interprétation de l'arithmétique dans certains groupes de permutations affines par morceaux d'un intervalle
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 8 / Issue 4 / October 2009
- Published online by Cambridge University Press:
- 30 January 2009, pp. 623-652
- Print publication:
- October 2009
-
- Article
- Export citation
GROUPS AND SEMIGROUPS WITH A ONE-COUNTER WORD PROBLEM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 197-209
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Circuits arithmétiques et calculs tensoriels
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 869-893
- Print publication:
- October 2008
-
- Article
- Export citation
Free algebras in varieties of BL-algebras generated by a BLn-chain
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 419-439
- Print publication:
- June 2006
-
- Article
-
- You have access
- Export citation
Everywhere Nonrecursive r.e. Sets in Recursively Presented Topological Spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 1 / February 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 105-128
- Print publication:
- February 1988
-
- Article
-
- You have access
- Export citation