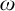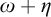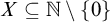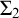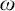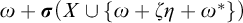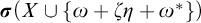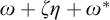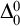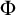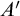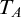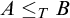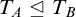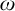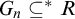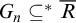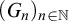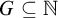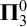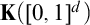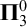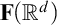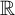Refine listing
Actions for selected content:
169 results in 03DXX
COMPARING COMPUTABILITY IN TWO TOPOLOGIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 1232-1250
- Print publication:
- September 2024
-
- Article
- Export citation
ON COHESIVE POWERS OF LINEAR ORDERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 13 March 2023, pp. 947-1004
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON CUPPING AND AHMAD PAIRS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 12 December 2022, pp. 1358-1369
- Print publication:
- September 2024
-
- Article
- Export citation
ON ROBUST THEOREMS DUE TO BOLZANO, WEIERSTRASS, JORDAN, AND CANTOR
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1077-1127
- Print publication:
- September 2024
-
- Article
- Export citation
PARTITION GENERICITY AND PIGEONHOLE BASIS THEOREMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 03 October 2022, pp. 829-857
- Print publication:
- June 2024
-
- Article
- Export citation
FINITIST AXIOMATIC TRUTH
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 22-73
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXPANDING THE REALS BY CONTINUOUS FUNCTIONS ADDS NO COMPUTATIONAL POWER
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 1083-1102
- Print publication:
- September 2023
-
- Article
- Export citation
THE TURING DEGREES AND KEISLER’S ORDER
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 07 September 2022, pp. 331-341
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MAXIMAL TOWERS AND ULTRAFILTER BASES IN COMPUTABILITY THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 15 August 2022, pp. 1170-1190
- Print publication:
- September 2023
-
- Article
- Export citation
ALMOST THEOREMS OF HYPERARITHMETIC ANALYSIS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 664-696
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PA RELATIVE TO AN ENUMERATION ORACLE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 18 July 2022, pp. 1497-1525
- Print publication:
- December 2023
-
- Article
- Export citation
COMPUTABLE REDUCIBILITY OF EQUIVALENCE RELATIONS AND AN EFFECTIVE JUMP OPERATOR
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 13 June 2022, pp. 540-561
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Undecidability of the Spectral Gap
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 June 2022, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE SIMPLEST LOW LINEAR ORDER WITH NO COMPUTABLE COPIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 June 2022, pp. 97-111
- Print publication:
- March 2024
-
- Article
- Export citation
A journey through computability, topology and analysis
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 28 June 2022, pp. 266-267
- Print publication:
- June 2022
-
- Article
-
- You have access
- Export citation
Point Degree Spectra of Represented Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 27 May 2022, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
UNIVERSAL CODING AND PREDICTION ON ERGODIC RANDOM POINTS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 28 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 02 May 2022, pp. 387-412
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRUCTURAL HIGHNESS NOTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 28 April 2022, pp. 1692-1724
- Print publication:
- December 2023
-
- Article
- Export citation
ON THE STRUCTURE OF COMPUTABLE REDUCIBILITY ON EQUIVALENCE RELATIONS OF NATURAL NUMBERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 April 2022, pp. 1038-1063
- Print publication:
- September 2023
-
- Article
- Export citation
ON THE UNCOUNTABILITY OF
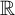 ${\mathbb R}$
${\mathbb R}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 07 April 2022, pp. 1474-1521
- Print publication:
- December 2022
-
- Article
- Export citation