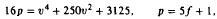Refine listing
Actions for selected content:
208 results in 11Axx
The least primitive root mod 2p2
- Part of
-
- Journal:
- Mathematika / Volume 45 / Issue 2 / December 1998
- Published online by Cambridge University Press:
- 26 February 2010, pp. 371-379
- Print publication:
- December 1998
-
- Article
- Export citation
On the quadratic reciprocity law
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 3 / December 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 423-425
- Print publication:
- December 1991
-
- Article
-
- You have access
- Export citation
Diophantine approximation by continued fractions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 324-330
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
Digit patterns and transcendental numbers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 216-236
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
On the existence of sequences of co-prime pairs of integers
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 84-89
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
An indeterminate in number theory
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 3 / June 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 469-472
- Print publication:
- June 1989
-
- Article
-
- You have access
- Export citation
On the largest component of an odd perfect number
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 42 / Issue 2 / April 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 280-286
- Print publication:
- April 1987
-
- Article
-
- You have access
- Export citation
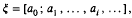
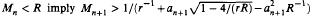 which generalizes a previous result of the author.
which generalizes a previous result of the author.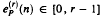 counts the number of occurrences (mod
counts the number of occurrences (mod 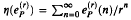 is transcendental except when
is transcendental except when 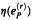 has infinite dimension over Q, where
has infinite dimension over Q, where