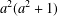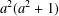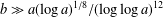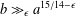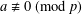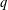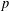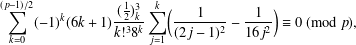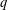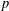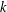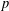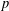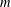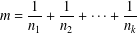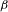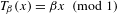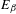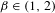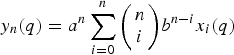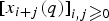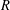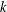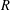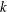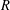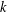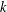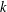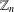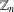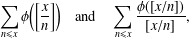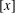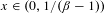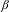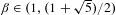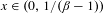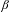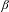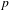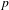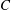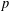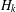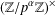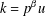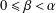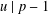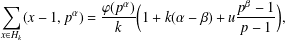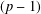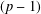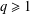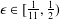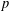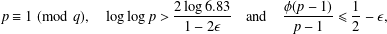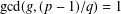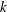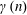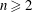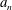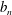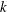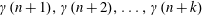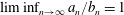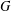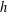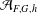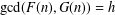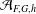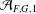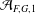Refine listing
Actions for selected content:
208 results in 11Axx
GAPS BETWEEN DIVISIBLE TERMS IN
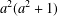 $a^{2}(a^{2}+1)$
$a^{2}(a^{2}+1)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 396-400
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
NEW SUPERCONGRUENCES INVOLVING PRODUCTS OF TWO BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 367-378
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
A
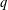 $q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
$q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 294-298
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
APPLICATIONS OF LERCH’S THEOREM TO PERMUTATIONS OF QUADRATIC RESIDUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 10 July 2019, pp. 362-371
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
A NOTE ON THE SUM OF RECIPROCALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 17 May 2019, pp. 189-193
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
THE NUMBER OF CYCLIC SUBGROUPS OF FINITE ABELIAN GROUPS AND MENON’S IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 201-206
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
The
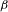 $\unicode[STIX]{x1D6FD}$-transformation with a hole at 0
$\unicode[STIX]{x1D6FD}$-transformation with a hole at 0
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2482-2514
- Print publication:
- September 2020
-
- Article
-
- You have access
- Open access
- Export citation
Positivity and continued fractions from the binomial transformation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 18 March 2019, pp. 831-847
- Print publication:
- June 2019
-
- Article
- Export citation
FACTORS OF CARMICHAEL NUMBERS AND AN EVEN WEAKER
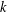 $k$-TUPLES CONJECTURE
$k$-TUPLES CONJECTURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 20 February 2019, pp. 376-384
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
ALTERNATING COLOURINGS OF THE VERTICES OF A REGULAR POLYGON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 177-181
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
NOTE ON SUMS INVOLVING THE EULER FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 07 February 2019, pp. 194-200
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Digit frequencies and self-affine sets with non-empty interior
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 19 December 2018, pp. 1755-1787
- Print publication:
- July 2020
-
- Article
- Export citation
Numbers with Almost all Convergents in a Cantor Set
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 03 December 2018, pp. 869-875
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
A NEW MENON’S IDENTITY FROM GROUP ACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 369-375
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
CONGRUENCES FOR THE
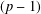 $(p-1)$TH APÉRY NUMBER
$(p-1)$TH APÉRY NUMBER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 362-368
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
QUADRATIC NONRESIDUES AND NONPRIMITIVE ROOTS SATISFYING A COPRIMALITY CONDITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 12 November 2018, pp. 177-183
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Consecutive Integers with Close Kernels
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 24 October 2018, pp. 469-473
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
On extensions of van Hamme's conjectures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 5 / October 2018
- Published online by Cambridge University Press:
- 30 August 2018, pp. 1017-1027
- Print publication:
- October 2018
-
- Article
- Export citation
ON NUMBERS
 $n$ WITH POLYNOMIAL IMAGE COPRIME WITH THE
$n$ WITH POLYNOMIAL IMAGE COPRIME WITH THE  $n$TH TERM OF A LINEAR RECURRENCE
$n$TH TERM OF A LINEAR RECURRENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 23-33
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Distribution of Class Numbers in Continued Fraction Families of Real Quadratic Fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 20 August 2018, pp. 1193-1212
-
- Article
- Export citation