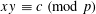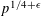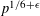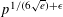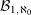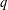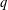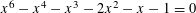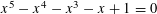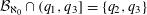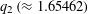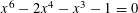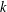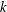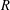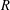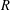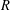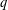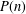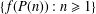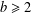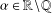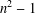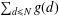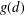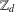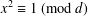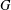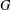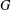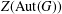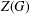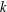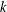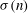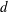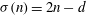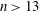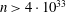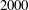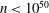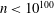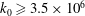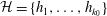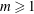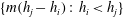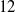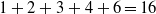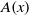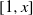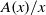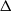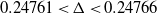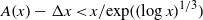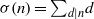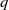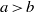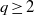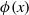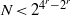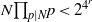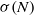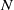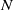Refine listing
Actions for selected content:
208 results in 11Axx
TOPICS IN DIVISIBILITY: PAIRWISE COPRIMALITY, THE GCD OF SHIFTED SETS AND POLYNOMIAL IRREDUCIBILITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 02 January 2016, pp. 167-168
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
SHORTEST DISTANCE IN MODULAR HYPERBOLA AND LEAST QUADRATIC NON-RESIDUE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 3 / 2016
- Published online by Cambridge University Press:
- 10 May 2016, pp. 860-865
- Print publication:
- 2016
-
- Article
- Export citation
ON SMALL BASES FOR WHICH 1 HAS COUNTABLY MANY EXPANSIONS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 362-377
- Print publication:
- 2016
-
- Article
- Export citation
FACTORS OF CARMICHAEL NUMBERS AND A WEAK
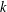 $k$-TUPLES CONJECTURE
$k$-TUPLES CONJECTURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 17 November 2015, pp. 421-429
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
STRONGLY
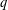 $q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR
$q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 17 November 2015, pp. 177-185
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
Two compact incremental prime sieves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 November 2015, pp. 675-683
-
- Article
-
- You have access
- Export citation
ON THE NUMBER OF DIVISORS OF
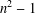 $n^{2}-1$
$n^{2}-1$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 02 October 2015, pp. 194-198
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
ON THE CENTRE OF THE AUTOMORPHISM GROUP OF A GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 16 June 2015, pp. 390-396
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
ON POWER MOMENTS OF THE HECKE MULTIPLICATIVE FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 25 March 2015, pp. 334-340
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
ON DEFICIENT-PERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 23 May 2014, pp. 186-194
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Wieferich pairs and Barker sequences, II
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 24-32
-
- Article
-
- You have access
- Export citation
A NOTE ON THE POLIGNAC NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 13 March 2014, pp. 500-502
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
COUNTING SYMMETRIC COLOURINGS OF THE VERTICES OF A REGULAR POLYGON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 January 2014, pp. 1-8
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
THE ERROR TERM IN THE COUNT OF ABUNDANT NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 43-65
- Print publication:
- January 2014
-
- Article
- Export citation
VARIATIONS ON A THEOREM OF DAVENPORT CONCERNING ABUNDANT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 12 September 2013, pp. 437-450
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
COUNTING SYMMETRIC BRACELETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 22 August 2013, pp. 431-436
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
PERFECT POWERS WITH THREE DIGITS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 06 August 2013, pp. 66-84
- Print publication:
- January 2014
-
- Article
- Export citation
IMPROVED UPPER BOUNDS FOR ODD MULTIPERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 12 June 2013, pp. 353-359
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
ADDITION TO ‘AN UPPER BOUND FOR THE NUMBER OF ODD MULTIPERFECT NUMBERS’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 07 June 2013, pp. 5-7
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
ON NEAR-PERFECT NUMBERS WITH TWO DISTINCT PRIME FACTORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 11 March 2013, pp. 520-524
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation