Refine listing
Actions for selected content:
208 results in 11Axx
ON THE CONSECUTIVE POWERS OF A PRIMITIVE ROOT: GAPS AND EXPONENTIAL SUMS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 08 November 2011, pp. 11-20
- Print publication:
- January 2012
-
- Article
- Export citation
AN EXTENSION OF SURY’S IDENTITY AND RELATED CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 04 October 2011, pp. 482-496
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
BOUNDS FOR ODD k-PERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 21 July 2011, pp. 475-480
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
ON A CURIOUS PROPERTY OF BELL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 153-158
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
ON LINEAR COMBINATIONS OF UNITS WITH BOUNDED COEFFICIENTS
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 2 / July 2011
- Published online by Cambridge University Press:
- 31 May 2011, pp. 247-262
- Print publication:
- July 2011
-
- Article
- Export citation
The least common multiple of consecutive arithmetic progression terms
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 2 / June 2011
- Published online by Cambridge University Press:
- 25 February 2011, pp. 431-441
-
- Article
-
- You have access
- Export citation
BOUNDS OF MULTIPLICATIVE CHARACTER SUMS WITH FERMAT QUOTIENTS OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 07 February 2011, pp. 456-462
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
ON COMMON DIVISORS OF MULTINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 13 October 2010, pp. 138-157
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
ON CARMICHAEL NUMBERS IN ARITHMETIC PROGRESSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 3 / June 2010
- Published online by Cambridge University Press:
- 26 April 2010, pp. 313-321
- Print publication:
- June 2010
-
- Article
-
- You have access
- Export citation
EXPANSION OF ORBITS OF SOME DYNAMICAL SYSTEMS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 07 April 2010, pp. 232-239
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
A REMARK ON PARTIAL SUMS INVOLVING THE MÖBIUS FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 13 January 2010, pp. 343-349
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
The Artin–Carmichael Primitive Root Problem on Average
- Part of
-
- Journal:
- Mathematika / Volume 55 / Issue 1-2 / December 2009
- Published online by Cambridge University Press:
- 21 December 2009, pp. 167-176
- Print publication:
- December 2009
-
- Article
- Export citation
ON m-COVERS AND m-SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 05 October 2009, pp. 223-235
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
SYLOW p-PSEUDOPRIMES TO SEVERAL BASES FOR SEVERAL PRIMES p
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 1 / February 2010
- Published online by Cambridge University Press:
- 05 October 2009, pp. 165-176
- Print publication:
- February 2010
-
- Article
-
- You have access
- Export citation
FLAT PRIMES AND THIN PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 26 April 2010, pp. 282-292
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Primes with an average sum of digits
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 271-292
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
ON THE DENSITY OF INTEGERS OF THE FORM (p−1)2−n IN ARITHMETIC PROGRESSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 431-436
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Integers Divisible by the Sum of their Prime Factors
- Part of
-
- Journal:
- Mathematika / Volume 52 / Issue 1-2 / December 2005
- Published online by Cambridge University Press:
- 21 December 2009, pp. 69-77
- Print publication:
- December 2005
-
- Article
- Export citation
On f(n) modulo Ω(n) and ω(n) when f is a polynomial
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-164
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
On extending Artin's conjecture to composite moduli
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 373-390
- Print publication:
- December 1999
-
- Article
- Export citation
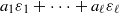
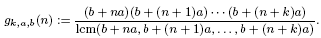
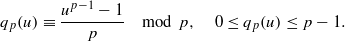
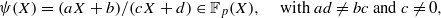
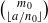 subsets
subsets 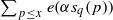 (where the sum is restricted to
(where the sum is restricted to 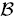 (
(