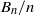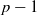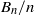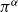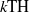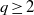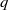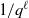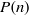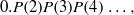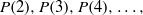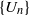Refine listing
Actions for selected content:
208 results in 11Axx
CARMICHAEL NUMBERS IN ARITHMETIC PROGRESSIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 2 / April 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 268-275
- Print publication:
- April 2013
-
- Article
-
- You have access
- Export citation
THE UNIVERSAL KUMMER CONGRUENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 106-132
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
UNCERTAINTY PRINCIPLES CONNECTED WITH THE MÖBIUS INVERSION FORMULA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 460-472
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
ON A SEQUENCE INVOLVING SUMS OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 197-205
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
ODD MULTIPERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 06 November 2012, pp. 56-63
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
CONSTRUCTION OF NORMAL NUMBERS USING THE DISTRIBUTION OF THE
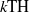 $k\rm TH$ LARGEST PRIME FACTOR
$k\rm TH$ LARGEST PRIME FACTOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 31 October 2012, pp. 158-168
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
CLASSIFICATION AND SYMMETRIES OF A FAMILY OF CONTINUED FRACTIONS WITH BOUNDED PERIOD LENGTH
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 03 May 2013, pp. 53-76
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
COMPLEX NUMBERS WITH BOUNDED PARTIAL QUOTIENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 16 April 2013, pp. 9-20
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON A VARIATION OF A CONGRUENCE OF SUBBARAO
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 04 February 2013, pp. 85-90
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON THE OPTIMAL CONTINUED FRACTION EXPANSION OF A QUADRATIC SURD
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 07 February 2013, pp. 133-156
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
A VARIANT OF HOFSTADTER’S SEQUENCE AND FINITE AUTOMATA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 03 May 2013, pp. 1-8
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON DIVISIBILITY OF BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 189-201
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
NOTE ON ODD MULTIPERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 17 September 2012, pp. 448-451
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
SOME PROPERTIES OF A SEQUENCE ANALOGOUS TO EULER NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 12 June 2012, pp. 425-440
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
THE LEAST COMMON MULTIPLE OF CONSECUTIVE TERMS IN A QUADRATIC PROGRESSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 389-404
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
SOME EXACT ALGEBRAIC EXPRESSIONS FOR THE TAILS OF TASOEV CONTINUED FRACTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 11 October 2012, pp. 179-193
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
On numbers n dividing the nth term of a linear recurrence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 271-289
-
- Article
-
- You have access
- Export citation
ON ODD PERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 16 February 2012, pp. 510-514
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
INFINITUDE OF ELLIPTIC CARMICHAEL NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 25 April 2012, pp. 45-60
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
A ONE LINE FACTORING ALGORITHM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2012, pp. 61-69
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation