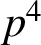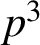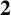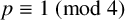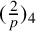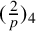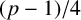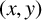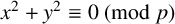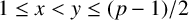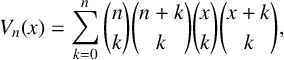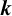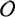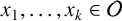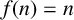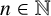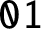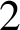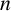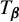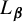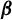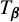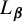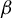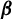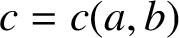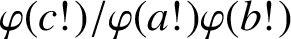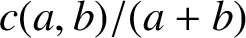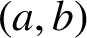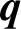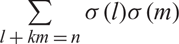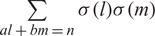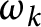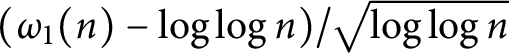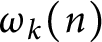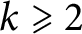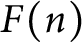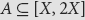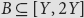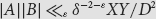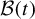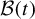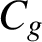Refine listing
Actions for selected content:
208 results in 11Axx
NEW GENERALISATIONS OF VAN HAMME’S (G.2) SUPERCONGRUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 18 May 2022, pp. 177-183
- Print publication:
- April 2023
-
- Article
- Export citation
Fractal projections with an application in number theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 16 March 2022, pp. 1760-1784
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NEW CHARACTERISATION FOR QUARTIC RESIDUACITY OF
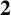 $\mathbf {2}$
$\mathbf {2}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 1-6
- Print publication:
- August 2022
-
- Article
- Export citation
ON THE DIVISIBILITY OF SUMS INVOLVING APÉRY-LIKE POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 14 March 2022, pp. 203-208
- Print publication:
- October 2022
-
- Article
- Export citation
Dilogarithm identities after Bridgeman
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 03 March 2022, pp. 1-23
- Print publication:
- January 2023
-
- Article
- Export citation
ON A
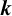 $\boldsymbol {k}$-ADDITIVE UNIQUENESS SET FOR MULTIPLICATIVE FUNCTIONS
$\boldsymbol {k}$-ADDITIVE UNIQUENESS SET FOR MULTIPLICATIVE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 209-214
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GAPS IN THE THUE–MORSE WORD
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 25 January 2022, pp. 110-144
- Print publication:
- February 2023
-
- Article
- Export citation
POINTS IN A FOLD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 7-17
- Print publication:
- August 2022
-
- Article
- Export citation
Dynamical behavior of alternate base expansions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 3 / March 2023
- Published online by Cambridge University Press:
- 22 December 2021, pp. 827-860
- Print publication:
- March 2023
-
- Article
- Export citation
AN EFFECTIVE ANALYTIC FORMULA FOR THE NUMBER OF DISTINCT IRREDUCIBLE FACTORS OF A POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 339-356
- Print publication:
- December 2022
-
- Article
- Export citation
ON QUOTIENTS OF VALUES OF EULER’S FUNCTION ON FACTORIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 November 2021, pp. 353-364
- Print publication:
- June 2022
-
- Article
- Export citation
A PROOF OF MERCA’S CONJECTURES ON SUMS OF ODD DIVISOR FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 10 September 2021, pp. 197-201
- Print publication:
- April 2022
-
- Article
- Export citation
A FAMILY OF
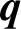 $\boldsymbol {q}$-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
$\boldsymbol {q}$-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 03 September 2021, pp. 296-302
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EVALUATION OF CONVOLUTION SUMS
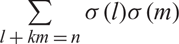 $$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND
$$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND 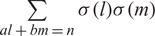 $$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
$$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 434-453
- Print publication:
- May 2022
-
- Article
- Export citation
CUBES IN FINITE FIELDS AND RELATED PERMUTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 15 July 2021, pp. 188-196
- Print publication:
- April 2022
-
- Article
- Export citation
Number of prime factors with a given multiplicity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 253-269
- Print publication:
- March 2022
-
- Article
- Export citation
Extremal problems for GCDs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 08 April 2021, pp. 922-929
-
- Article
-
- You have access
- Open access
- Export citation
The bifurcation locus for numbers of bounded type
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 08 April 2021, pp. 2239-2269
- Print publication:
- July 2022
-
- Article
- Export citation
ADDITIVE BASES AND NIVEN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 25 March 2021, pp. 373-380
- Print publication:
- December 2021
-
- Article
- Export citation
A lower bound for Cusick’s conjecture on the digits of n + t
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 24 February 2021, pp. 139-161
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation