Refine listing
Actions for selected content:
140 results in 11Lxx
EXPONENTIAL SUMS OVER PRIMES IN SHORT INTERVALS AND AN APPLICATION TO THE WARING–GOLDBACH PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 508-523
- Print publication:
- 2016
-
- Article
- Export citation
STRONGLY
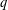 $q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR
$q$-ADDITIVE FUNCTIONS AND DISTRIBUTIONAL PROPERTIES OF THE LARGEST PRIME FACTOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 17 November 2015, pp. 177-185
- Print publication:
- April 2016
-
- Article
-
- You have access
- Export citation
SYSTEMS OF CONGRUENCES WITH PRODUCTS OF VARIABLES FROM SHORT INTERVALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 11 November 2015, pp. 364-371
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
Sub-Weyl subconvexity for Dirichlet
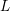 $L$-functions to prime power moduli
$L$-functions to prime power moduli
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 825-875
- Print publication:
- April 2016
-
- Article
- Export citation
Rational points on linear slices of diagonal hypersurfaces
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 218 / June 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 51-100
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
On the distribution of Atkin and Elkies primes for reductions of elliptic curves on average
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 April 2015, pp. 308-322
-
- Article
-
- You have access
- Export citation
THE NUMBER OF SOLUTIONS TO MORDELL’S EQUATION IN CONSTRAINED RANGES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 05 December 2014, pp. 708-718
- Print publication:
- September 2015
-
- Article
- Export citation
Galois representations attached to moments of Kloosterman sums and conjectures of Evans
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 07 October 2014, pp. 68-120
- Print publication:
- January 2015
-
- Article
- Export citation
ON THE EXPONENT OF DISTRIBUTION OF THE TERNARY DIVISOR FUNCTION
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 02 June 2014, pp. 121-144
- Print publication:
- January 2015
-
- Article
- Export citation
MULTIPLE EXPONENTIAL AND CHARACTER SUMS WITH MONOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 27 May 2014, pp. 363-373
- Print publication:
- July 2014
-
- Article
- Export citation
Double Character Sums over Subgroups and Intervals
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 15 May 2014, pp. 376-390
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
THE INTERSECTION OF PIATETSKI-SHAPIRO SEQUENCES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 347-362
- Print publication:
- July 2014
-
- Article
- Export citation
THE VALUE DISTRIBUTION OF INCOMPLETE GAUSS SUMS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 19 February 2013, pp. 381-398
- Print publication:
- July 2013
-
- Article
- Export citation
ON A CONJECTURE OF IGUSA
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 07 February 2013, pp. 399-425
- Print publication:
- July 2013
-
- Article
- Export citation
ON SELMER GROUPS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH A TWO-TORSION OVER
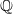 $\mathbb {Q}$
$\mathbb {Q}$
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 15 January 2013, pp. 303-319
- Print publication:
- July 2013
-
- Article
- Export citation
THE DISTRIBUTION OF THE MAXIMUM OF CHARACTER SUMS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 2 / July 2013
- Published online by Cambridge University Press:
- 08 January 2013, pp. 427-442
- Print publication:
- July 2013
-
- Article
- Export citation
THE RESONANCE METHOD FOR LARGE CHARACTER SUMS
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 11 September 2012, pp. 87-118
- Print publication:
- January 2013
-
- Article
- Export citation
ON SELMER GROUPS AND TATE–SHAFAREVICH GROUPS FOR ELLIPTIC CURVES y2=x3−n3
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 236-274
- Print publication:
- July 2012
-
- Article
- Export citation
A PAUCITY ESTIMATE RELATED TO NEWTON SUMS OF ODD DEGREE
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 27 March 2012, pp. 225-235
- Print publication:
- July 2012
-
- Article
- Export citation
HUA-TYPE ITERATION FOR MULTIDIMENSIONAL WEYL SUMS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 27 March 2012, pp. 209-224
- Print publication:
- July 2012
-
- Article
- Export citation

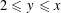
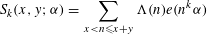
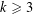



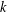
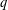
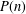
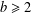
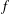
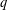
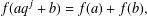
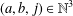
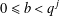
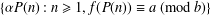
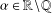
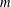
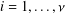
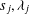
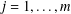
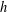
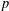
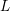
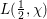
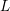
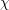
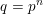
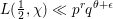

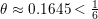
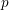
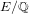
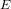


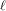
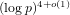
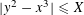
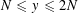
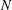
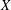
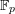
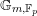
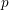
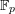

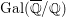
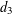
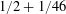
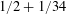
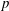
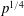
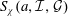
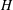
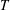
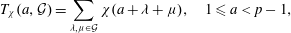
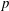
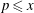
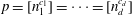
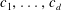
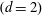
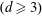
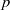
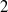
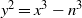
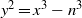
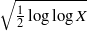
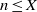
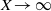
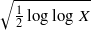 as
as 