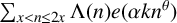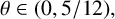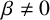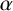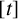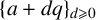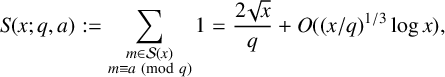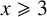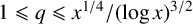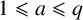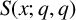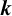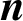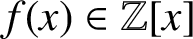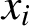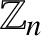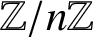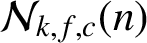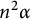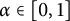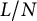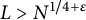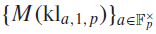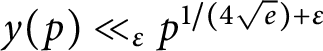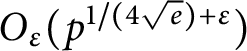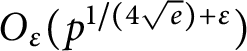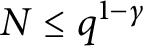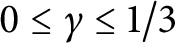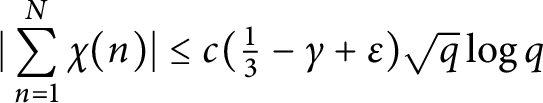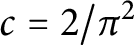Refine listing
Actions for selected content:
143 results in 11Lxx
AVERAGES OF EXPONENTIAL TWISTS OF THE VON MANGOLDT FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 25 April 2022, pp. 425-430
- Print publication:
- December 2022
-
- Article
- Export citation
ON THE INHOMOGENEOUS VINOGRADOV SYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 396-403
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DIVISOR FUNCTION OVER NONHOMOGENEOUS BEATTY SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 280-287
- Print publication:
- October 2022
-
- Article
- Export citation
DISTRIBUTION OF ELEMENTS OF A FLOOR FUNCTION SET IN ARITHMETICAL PROGRESSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 01 March 2022, pp. 419-424
- Print publication:
- December 2022
-
- Article
- Export citation
LOWER-ORDER TERMS OF THE ONE-LEVEL DENSITY OF A FAMILY OF QUADRATIC HECKE
 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 22 February 2022, pp. 178-221
-
- Article
- Export citation
APPLICATIONS OF CIRCULANT MATRICES TO DETERMINANTS INVOLVING
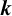 $\boldsymbol {k}$TH POWER RESIDUES
$\boldsymbol {k}$TH POWER RESIDUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 09 February 2022, pp. 243-253
- Print publication:
- October 2022
-
- Article
- Export citation
A generalized Davenport expansion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 26 August 2021, pp. 711-715
-
- Article
- Export citation
SUMS OF POLYNOMIAL-TYPE EXCEPTIONAL UNITS MODULO
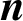 $\boldsymbol {n}$
$\boldsymbol {n}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 21 July 2021, pp. 202-211
- Print publication:
- April 2022
-
- Article
- Export citation
The distribution of the maximum of partial sums of Kloosterman sums and other trace functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 28 June 2021, pp. 1610-1651
- Print publication:
- July 2021
-
- Article
- Export citation
Une note sur la densité des zéros des sommes partielles de la fonction zeta de Dedekind sur un corps quadratique
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 409-415
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the triple correlations of fractional parts of
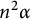 $n^2\alpha $
$n^2\alpha $
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 04 May 2021, pp. 1347-1384
- Print publication:
- October 2022
-
- Article
- Export citation
On the size of the maximum of incomplete Kloosterman sums
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 15 April 2021, pp. 563-590
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
Subproducts of small residue classes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 13 January 2021, pp. 1-8
- Print publication:
- March 2022
-
- Article
- Export citation
The second moment of symmetric square L-functions over Gaussian integers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 January 2021, pp. 54-80
- Print publication:
- February 2022
-
- Article
- Export citation
A Pólya–Vinogradov inequality for short character sums
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 906-910
- Print publication:
- December 2021
-
- Article
- Export citation
EXPONENTIAL SUMS AND ADDITIVE COMBINATORICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 506-508
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
ONE-LEVEL DENSITY OF LOW-LYING ZEROS OF QUADRATIC HECKE L-FUNCTIONS OF IMAGINARY QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 112 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 29 October 2020, pp. 170-192
-
- Article
- Export citation
Autocorrelation functions for quantum particles in supersymmetric Pöschl-Teller potentials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 October 2020, pp. 840-852
- Print publication:
- December 2021
-
- Article
- Export citation
DISTRIBUTION OF INTEGERS WITH PRESCRIBED STRUCTURE AND APPLICATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 19 October 2020, pp. 509-511
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Primitive rational points on expanding horocycles in products of the modular surface with the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 04 June 2020, pp. 1706-1750
- Print publication:
- June 2021
-
- Article
- Export citation